Advertisements
Advertisements
प्रश्न
The following table gives the activities of a project and their duration in days
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 5 |
| Duration | 5 | 8 | 6 | 7 | 5 | 4 | 8 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
उत्तर
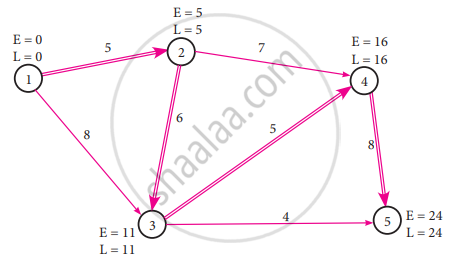
E1 = 0
E2 = 0 + 5 = 5
E3 = (0 + 8) or (5 + 6)
Whichever is maximum
= 11
E4 = (11 + 5) or (5 + 7)
Whichever is maximum
= 16
E5 = (11 + 4) or (16 + 8)
Whichever is maximum
= 24
L5 = 24
L4 = 24 – 8 = 16
L3 = (24 – 4) or (16 – 5)
whichever is minimum
= 11
L2 = (16 – 6) or (16 – 7)
whichever is minimum
= 5
L1 = (5 – 5) or (11 – 8)
whichever is minimum
L1 = 0
| Activity | Duration tij |
EST | EFT = EST + tij | LST = LFT – tij | LFT |
| 1 - 2 | 5 | 0 | 5 | 5 – 5 = 0 | 5 |
| 1 - 3 | 8 | 0 | 8 | 11 – 8 = 3 | 11 |
| 2 - 3 | 6 | 5 | 11 | 11 – 6 = 5 | 11 |
| 2 - 4 | 7 | 5 | 12 | 16 – 7 = 9 | 16 |
| 3 - 4 | 5 | 11 | 16 | 16 – 5 = 11 | 16 |
| 3 - 5 | 4 | 11 | 15 | 24 – 4 = 20 | 24 |
| 4 - 5 | 8 | 16 | 24 | 24 – 8 = 16 | 24 |
Since EFT and LFT are same in 1 - 2, 2 - 3, 3 - 4 and 4 - 5.
Hence the critical path is 1 - 2 - 3 - 4 - 5 and the duration time taken is 24 days.
APPEARS IN
संबंधित प्रश्न
Draw the network for the project whose activities with their relationships are given below:
Activities A, D, E can start simultaneously; B, C > A; G, F > D, C; H > E, F.
A project schedule has the following characteristics
| Activity | 1 - 2 | 1 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 9 | 5 - 6 | 5 - 7 | 6 - 8 | 7 - 8 | 8 - 10 | 9 - 10 |
| Time | 4 | 1 | 1 | 1 | 6 | 5 | 4 | 8 | 1 | 2 | 5 | 7 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
The following table use the activities in a construction projects and relevant information
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 2 - 4 | 3 - 4 | 4 - 5 |
| Duration (in days) |
22 | 27 | 12 | 14 | 6 | 12 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
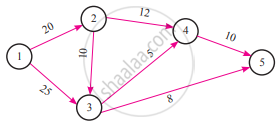
The critical path of the following network is
One of the conditions for the activity (i, j) to lie on the critical path is
In a network while numbering the events which one of the following statements is false?
Which of the following is not correct?
The objective of network analysis is to
In critical path analysis, the word CPM mean
Draw the network diagram for the following activities.
| Activity code | A | B | C | D | E | F | G |
| Predecessor activity | - | - | A | A | B | C | D, E |
