Advertisements
Advertisements
प्रश्न
The following table shows the production of gasoline in U.S.A. for the years 1962 to 1976.
| Year | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
| Production (million barrels) |
0 | 0 | 1 | 1 | 2 | 3 | 4 | 5 |
| Year | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | |
| Production (million barrels) |
6 | 7 | 8 | 9 | 8 | 9 | 10 |
- Obtain trend values for the above data using 5-yearly moving averages.
- Plot the original time series and trend values obtained above on the same graph.
उत्तर
a. We construct the following table to obtain 5 yearly moving average:
| Year 't' |
Production (millions of barrels) yt |
5-yearly moving total |
5-yearly moving averages trend value |
| 1962 | 0 | – | – |
| 1963 | 0 | – | – |
| 1964 | 1 | 4 | 0.8 |
| 1965 | 1 | 7 | 1.4 |
| 1966 | 2 | 11 | 2.2 |
| 1967 | 3 | 15 | 3.0 |
| 1968 | 4 | 20 | 4.0 |
| 1969 | 5 | 25 | 5.0 |
| 1970 | 6 | 30 | 6.0 |
| 1971 | 7 | 35 | 7.0 |
| 1972 | 8 | 38 | 7.6 |
| 1973 | 9 | 41 | 8.2 |
| 1974 | 8 | 44 | 8.8 |
| 1975 | 9 | – | – |
| 1976 | 10 | – | – |
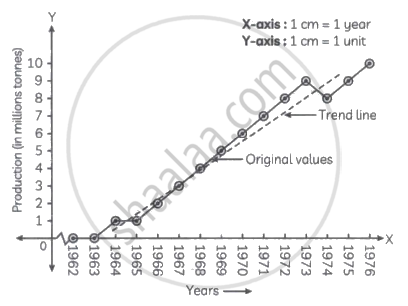
b. Taking year on X-axis and production trend on Y-axis, we plot the points for production corresponding to years to get the graph of time series and plot the point for trend values corresponding to years to get the graph of trend as shown below:
APPEARS IN
संबंधित प्रश्न
Obtain the trend line for the above data using 5 yearly moving averages.
Obtain the trend values for the data in using 4-yearly centered moving averages.
| Year | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 |
| Index | 0 | 2 | 3 | 3 | 2 | 4 | 5 | 6 | 7 | 10 |
Obtain the trend values for the above data using 3-yearly moving averages.
Choose the correct alternative :
We can use regression line for past data to forecast future data. We then use the line which_______.
Choose the correct alternative :
Which of the following is a major problem for forecasting, especially when using the method of least squares?
Fill in the blank :
The method of measuring trend of time series using only averages is _______
Fill in the blank :
The complicated but efficient method of measuring trend of time series is _______.
State whether the following is True or False :
Moving average method of finding trend is very complicated and involves several calculations.
State whether the following is True or False :
All the three methods of measuring trend will always give the same results.
Solve the following problem :
Following table shows the amount of sugar production (in lac tonnes) for the years 1971 to 1982.
| Year | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
| Production | 1 | 0 | 1 | 2 | 3 | 2 | 3 | 6 | 5 | 1 | 4 | 10 |
Fit a trend line to the above data by graphical method.
Solve the following problem :
Fit a trend line to data in Problem 4 by the method of least squares.
Solve the following problem :
Following table shows the number of traffic fatalities (in a state) resulting from drunken driving for years 1975 to 1983.
| Year | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 |
| No. of deaths | 0 | 6 | 3 | 8 | 2 | 9 | 4 | 5 | 10 |
Fit a trend line to the above data by graphical method.
Solve the following problem :
Obtain trend values for data in Problem 13 using 4-yearly moving averages.
Solve the following problem :
Following table shows the all India infant mortality rates (per ‘000) for years 1980 to 2010.
| Year | 1980 | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 |
| IMR | 10 | 7 | 5 | 4 | 3 | 1 | 0 |
Fit a trend line to the above data by graphical method.
Solve the following problem :
Following tables shows the wheat yield (‘000 tonnes) in India for years 1959 to 1968.
| Year | 1959 | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 |
| Yield | 0 | 1 | 2 | 3 | 1 | 0 | 4 | 1 | 2 | 10 |
Fit a trend line to the above data by the method of least squares.
The complicated but efficient method of measuring trend of time series is ______
The simplest method of measuring trend of time series is ______
The method of measuring trend of time series using only averages is ______
Use the method of least squares to fit a trend line to the data given below. Also, obtain the trend value for the year 1975.
| Year | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
| Production (million barrels) |
0 | 0 | 1 | 1 | 2 | 3 | 4 | 5 |
| Year | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 | |
| Production (million barrels) |
6 | 8 | 9 | 9 | 8 | 7 | 10 |
Complete the table using 4 yearly moving average method.
| Year | Production | 4 yearly moving total |
4 yearly centered total |
4 yearly centered moving average (trend values) |
| 2006 | 19 | – | – | |
| `square` | ||||
| 2007 | 20 | – | `square` | |
| 72 | ||||
| 2008 | 17 | 142 | 17.75 | |
| 70 | ||||
| 2009 | 16 | `square` | 17 | |
| `square` | ||||
| 2010 | 17 | 133 | `square` | |
| 67 | ||||
| 2011 | 16 | `square` | `square` | |
| `square` | ||||
| 2012 | 18 | 140 | 17.5 | |
| 72 | ||||
| 2013 | 17 | 147 | 18.375 | |
| 75 | ||||
| 2014 | 21 | – | – | |
| – | ||||
| 2015 | 19 | – | – |
Obtain the trend values for the following data using 5 yearly moving averages:
| Year | 2000 | 2001 | 2002 | 2003 | 2004 |
| Production xi |
10 | 15 | 20 | 25 | 30 |
| Year | 2005 | 2006 | 2007 | 2008 | 2009 |
| Production xi |
35 | 40 | 45 | 50 | 55 |
The following table shows gross capital information (in Crore ₹) for years 1966 to 1975:
| Years | 1966 | 1967 | 1968 | 1969 | 1970 |
| Gross Capital information | 20 | 25 | 25 | 30 | 35 |
| Years | 1971 | 1972 | 1973 | 1974 | 1975 |
| Gross Capital information | 30 | 45 | 40 | 55 | 65 |
Obtain trend values using 5-yearly moving values.
Complete the following activity to fit a trend line to the following data by the method of least squares.
| Year | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 |
| Number of deaths | 0 | 6 | 3 | 8 | 2 | 9 | 4 | 5 | 10 |
Solution:
Here n = 9. We transform year t to u by taking u = t - 1979. We construct the following table for calculation :
| Year t | Number of deaths xt | u = t - 1979 | u2 | uxt |
| 1975 | 0 | - 4 | 16 | 0 |
| 1976 | 6 | - 3 | 9 | - 18 |
| 1977 | 3 | - 2 | 4 | - 6 |
| 1978 | 8 | - 1 | 1 | - 8 |
| 1979 | 2 | 0 | 0 | 0 |
| 1980 | 9 | 1 | 1 | 9 |
| 1981 | 4 | 2 | 4 | 8 |
| 1982 | 5 | 3 | 9 | 15 |
| 1983 | 10 | 4 | 16 | 40 |
| `sumx_t` =47 | `sumu`=0 | `sumu^2=60` | `square` |
The equation of trend line is xt= a' + b'u.
The normal equations are,
`sumx_t = na^' + b^' sumu` ...(1)
`sumux_t = a^'sumu + b^'sumu^2` ...(2)
Here, n = 9, `sumx_t = 47, sumu= 0, sumu^2 = 60`
By putting these values in normal equations, we get
47 = 9a' + b' (0) ...(3)
40 = a'(0) + b'(60) ...(4)
From equation (3), we get a' = `square`
From equation (4), we get b' = `square`
∴ the equation of trend line is xt = `square`
Following table gives the number of road accidents (in thousands) due to overspeeding in Maharashtra for 9 years. Complete the following activity to find the trend by the method of least squares.
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| Number of accidents | 39 | 18 | 21 | 28 | 27 | 27 | 23 | 25 | 22 |
Solution:
We take origin to 18, we get, the number of accidents as follows:
| Year | Number of accidents xt | t | u = t - 5 | u2 | u.xt |
| 2008 | 21 | 1 | -4 | 16 | -84 |
| 2009 | 0 | 2 | -3 | 9 | 0 |
| 2010 | 3 | 3 | -2 | 4 | -6 |
| 2011 | 10 | 4 | -1 | 1 | -10 |
| 2012 | 9 | 5 | 0 | 0 | 0 |
| 2013 | 9 | 6 | 1 | 1 | 9 |
| 2014 | 5 | 7 | 2 | 4 | 10 |
| 2015 | 7 | 8 | 3 | 9 | 21 |
| 2016 | 4 | 9 | 4 | 16 | 16 |
| `sumx_t=68` | - | `sumu=0` | `sumu^2=60` | `square` |
The equation of trend is xt =a'+ b'u.
The normal equations are,
`sumx_t=na^'+b^'sumu ...(1)`
`sumux_t=a^'sumu+b^'sumu^2 ...(2)`
Here, n = 9, `sumx_t=68,sumu=0,sumu^2=60,sumux_t=-44`
Putting these values in normal equations, we get
68 = 9a' + b'(0) ...(3)
∴ a' = `square`
-44 = a'(0) + b'(60) ...(4)
∴ b' = `square`
The equation of trend line is given by
xt = `square`
