Advertisements
Advertisements
प्रश्न
The inequality representing the following graph is ______.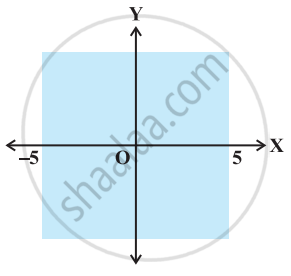
पर्याय
|x| < 5
|x| ≤ 5
|x| > 5
|x| ≥ 5
उत्तर
The inequality representing the following graph is |x| < 5.
Explanation:
The given graph represents x > –5 and x < 5.
Combining the two inequalities |x| < 5.
APPEARS IN
संबंधित प्रश्न
Solve 24x < 100, when x is an integer.
Solve –12x > 30, when x is a natural number.
Solve –12x > 30, when x is an integer.
Solve the given inequality for real x: 3x – 7 > 5x – 1.
Solve the given inequality for real x: 3(x – 1) ≤ 2 (x – 3)
Solve the given inequality for real x: 3(2 – x) ≥ 2(1 – x)
Solve the given inequality for real x : `x/3 > x/2 + 1`
Solve the given inequality for real x : `(3(x-2))/5 <= (5(2-x))/3`
Solve the given inequality for real x: `1/2 ((3x)/5 + 4) >= 1/3 (x -6)`
Solve the given inequality for real x: 2(2x + 3) – 10 < 6 (x – 2)
Solve the given inequality for real x: 37 – (3x + 5) ≥ 9x – 8(x – 3)
Solve the given inequality for real x: `x/4 < (5x - 2)/3 - (7x - 3)/5`
Solve the given inequality for real x: `((2x- 1))/3 >= ((3x - 2))/4 - ((2 - x))/5`
Solve the given inequality and show the graph of the solution on number line:
3(1 – x) < 2 (x + 4)
Solve the given inequality and show the graph of the solution on number line:
`x/2 >= ((5x -2))/3 - ((7x - 3))/5`
Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5 cm longer than the second?
[Hint: If x is the length of the shortest board, then x, (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x = (x + 3) + 2x ≤ 91 and 2x ≥ (x + 3) + 5]
Solve the inequality.
`-3 <= 4 - (7x)/2 <= 18`
Represent to solution set of each of the following inequations graphically in two dimensional plane:
x + 2y − y ≤ 0
Represent to solution set of each of the following inequations graphically in two dimensional plane:
5. −3x + 2y ≤ 6
Represent to solution set of each of the following inequations graphically in two dimensional plane:
6. x ≤ 8 − 4y
Represent to solution set of each of the following inequations graphically in two dimensional plane:
y ≥ 2x − 8
State whether the following statement is True or False.
If x > y and b < 0, then bx < by
State whether the following statement is True or False.
Graph of x > –2 is
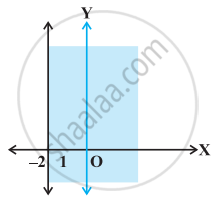
If x > –2 and x < 9, then x ∈ (– 2, 9)
If |x| > 5, then x ∈ (– `oo`, – 5) ∪ [5, `oo`)
If |x| ≤ 4, then x ∈ [– 4, 4]
