Advertisements
Advertisements
प्रश्न
The polygon in which sum of all exterior angles is equal to the sum of interior angles is called ______.
उत्तर
The polygon in which sum of all exterior angles is equal to the sum of interior angles is called quadrilateral.
Explanation:
We know that, the sum of exterior angles of a polygon is 360° and in a quadrilateral, sum of interior angles is also 360°.
Therefore, a quadrilateral is a polygon in which the sum of both interior and exterior angles are equal.
APPEARS IN
संबंधित प्रश्न
Find the angle measure x in the given Figure
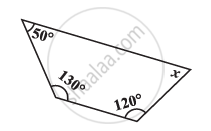
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13 Find all the angles of the quadrilateral.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

Diagonals necessarily bisect opposite angles in a
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is ______.
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
