Advertisements
Advertisements
प्रश्न
The ratio of fruit trees and vegetable trees in an orchard is 3:4. If 6 more trees of each type are planted, the ratio of trees would be 6:7. Find the number of fruit trees and vegetable trees in the orchard.
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees= 3x and the number of vegetable trees = `square`
From the given condition,
`(3x + square)/(square + square) = square/square`
`square (3x + square) = square (square + square)`
`square + square = square + square`
`square - square = square - square`
`- square = - square`
`square = square`
x = `square`
∴ Number of fruit trees in the orchard = 3x = 3 × `square` = `square` and number of vegetable trees in the orchard = 4x = 4 × `square` = `square`
Hence, the number of fruit trees and vegetable trees in the orchard are `square` and `square` respectively.
उत्तर
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees = 3x and the number of vegetable trees = 4x
From the given condition,
`(3x + bb6)/(bb(4x) + bb6) = bb6/bb7`
7(3x + 6) = 6 (4x + 6)
21x + 42 = 24x + 36
21x – 24x = 36 – 42
– 3x = – 6
3x = 6
x = 2
∴ Number of fruit trees in the orchard = 3x = 3 × 2 = 6 and number of vegetable trees in the orchard = 4x = 4 × 2 = 8
Hence, the number of fruit trees and vegetable trees in the orchard are 6 and 8 respectively.
APPEARS IN
संबंधित प्रश्न
The roots of the quadratic equation `2x^2-x-6=0`
(a)`-2, 3/2` (b) `2, -3/2`
(c)` -2, 3/2` (d) `2, 3/2`
Show the x= -3 is a solution of `x^2+6x+9=0`
If one root of the quadratic equation `3x^2-10x+k=0` is reciprocal of the other , find the value of k.
Solve` 2x^2+ax-a^2=0`
Solve `3x^2+5sqrt5x-10=0`
Solve `sqrt3x^2+10x-8sqrt3=0`
Solve for x: `3x^2-2sqrt6x+2=0`
Write any two quadratic equations.
Decide whether the following equation is quadratic equation or not.
x2 + 5x – 2 = 0
Decide whether the following equation is quadratic equation or not.
y2 = 5y – 10
Choose the correct answer for the following question.
Out of the following equations, find the equation having the sum of its roots –5.
Ranjana wants to distribute 540 oranges among some students. If 30 students were more each would get 3 oranges less. Find the number of students.
If P(y) = y² - 2y + 5, find P(2) .
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
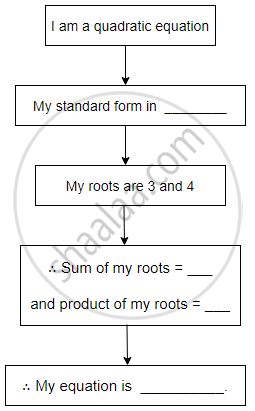
Complete the following activity to form a quadratic equation.
Activity:
Construct a word problem on quadratic equation, such that one of its answers is 20 (years, rupees, centimeter, etc.). Also, solve it.
Find c if the system of equations cx + 3y + (3 – c) = 0; 12x + cy – c = 0 has infinitely many solutions?
Solve for x : `1/(2a + b + 2x) =1/(2a) + 1/b + 1/(2x); x ≠ 0, x ≠ (−2a −b)/2`, a, b ≠ 0
Mukund has ₹ 50 more than Sagar. If the product of the amount they have is 15,000, then find the amount each has
A tank can be filled up by two taps in 6 hours. The smaller tap alone takes 5 hours more than the bigger tap alone. Find the time required by each tap to fill the tank separately.
