Advertisements
Advertisements
प्रश्न
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
उत्तर
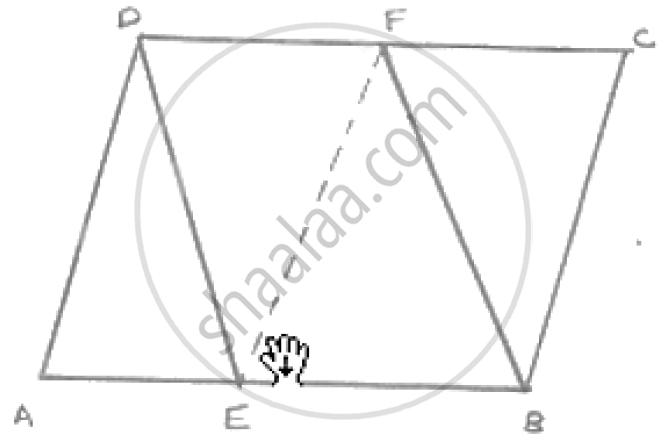
Since ABCD is a parallelogram
∴AB || DC and AB = DC
⇒EB || DF and `1/2` AB =`1/2` DC
⇒EB || DF and EB = DF
EBFD is a parallelogram
APPEARS IN
संबंधित प्रश्न
ABCD is a square. AC and BD intersect at O. State the measure of ∠AOB.
P and Q are the points of trisection of the diagonal BD of a parallelogram AB Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a
parallelogram.
In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.
Prove that (i) ∠PAC = ∠BCA (ii) ABCP is a parallelogram
In a parallelogram ABCD, if ∠D = 115°, then write the measure of ∠A.
In a parallelogram ABCD, if ∠A = (3x − 20)°, ∠B = (y + 15)°, ∠C = (x + 40)°, then find the values of xand y.
In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Find AB : AD.
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
In the given Figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF. (Use congruent property of triangles)
