Advertisements
Advertisements
प्रश्न
The slope of a line joining P(6, k) and Q(1 – 3k, 3) is `1/2`. Find:
- k.
- mid-point of PQ, using the value of ‘k’ found in (i).
उत्तर
i. Slope of PQ = `(3 - k)/(1 - 3k - 6)`
`=> 1/2 = (3 - k)/(-3k - 5)`
`=>` –3k – 5 = 2(3 – k)
`=>` –3k – 5 = 6 – 2k
`=>` –3k + 2k = 6 + 5
`=>` –k = 11
`=>` k = –11
ii. Substituting k in P and Q, we get
P(6, k) = (6, –11)
And Q(1 – 3k, 3) = (1 – 3(–11), 3)
= (1 + 33, 3)
= (34, 3)
∴ Midpoint of PQ = `((6 + 34)/2, (-11 + 3)/2)`
= `(40/2, (-8)/2)`
= (20, −4)
APPEARS IN
संबंधित प्रश्न
Find the slope of the line with inclination 30° .
Find the value(s) of k so that PQ will be parallel to RS. Given : P(5, −1), Q(6, 11), R(6, −4k) and S(7, k2)
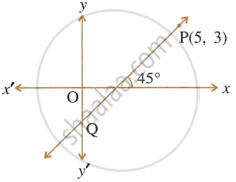
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
Find the slope of the line which is parallel to x + 2y + 3 = 0
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
90°
Determine whether the following point is collinear.
D(–2, –3), E(1, 0), F(2, 1)
Find the slope of a line passing through the given pair of points (3,7) and (5,13)
Find the slope and the y-intercept of the following line 3x + y = 7
Find the slope and the y-intercept of the following line x - 2 = `(5 - 3"y")/2`
A line passing through the points (a, 2a) and (- 2, 3) is perpendicular to the line 4a + 3y + 5 = 0. Find the value of a.
