Advertisements
Advertisements
प्रश्न
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is ______.
पर्याय
5
– 5
`(-1)/5`
`1/5`
उत्तर
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is 5.
Explanation:
y = 3x2 – x + 1
∴ Slope of a tangent = `(dy)/(dx)` = 6x – 1
∴ `((dy)/(dx))_((1, 3)` = 6 × 1 – 1 = 5
APPEARS IN
संबंधित प्रश्न
Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by the ellipse `x^2/16 + y^2/9 = 1.`
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is ______.
Find the area under the given curve and given line:
y = x4, x = 1, x = 5 and x-axis
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = x4, x = 1, x = 5
State whether the following is True or False :
The area bounded by the curve y = f(x), X-axis and lines x = a and x = b is `|int_"a"^"b" f(x)*dx|`.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
Choose the correct alternative:
Area of the region bounded by y2 = 16x, x = 1 and x = 4 and the X axis, lying in the first quadrant is ______
Choose the correct alternative:
Area of the region bounded by x = y4, y = 1 and y = 5 and the Y-axis lying in the first quadrant is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find area of the region bounded by the curve y = – 4x, the X-axis and the lines x = – 1 and x = 2
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
Find the area of the region bounded by the curve y = `sqrt(36 - x^2)`, the X-axis lying in the first quadrant and the lines x = 0 and x = 6
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
The area of the circle `x^2 + y^2 = 16`, exterior to the parabola `y = 6x`
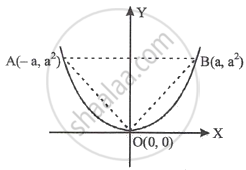
The figure shows as triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x2 is equal to ______.
The area bounded by the curve, y = –x, X-axis, x = 1 and x = 4 is ______.
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
