Advertisements
Advertisements
प्रश्न
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Advertisements
उत्तर
For the given curves, the graph is as follows:
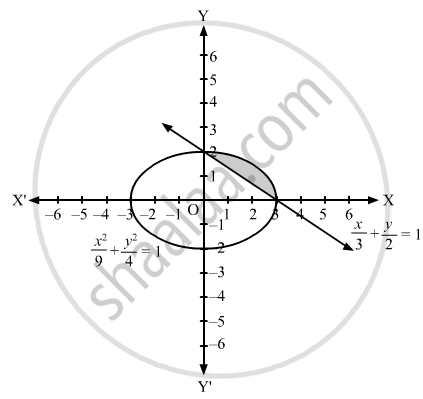
Area of the region bounded by the given curves:
\[\frac{2}{3} \int_0^3 \sqrt{9 - x^2} d x - \frac{1}{3} \int_0^3 (6 - 2x) d x = \frac{2}{3} \left[ \frac{x}{2}\sqrt{9 - x^2} + \frac{9}{2} \sin^{- 1} \frac{x}{3} \right]_0^3 - \frac{1}{3} \left[ 6x - x^2 \right]_0^3 \]
\[ = \frac{2}{3}\left[ \frac{9}{2} \times \frac{\pi}{2} \right] - \frac{1}{3}\left[ 18 - 9 \right]\]
\[ = \left( \frac{3\pi}{2} - 3 \right) \text { sq units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the ellipse `x^2/16 + y^2/9 = 1.`
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area between the curves y = x and y = x2
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Find the area bounded by the circle x2 + y2 = 16 and the line `sqrt3 y = x` in the first quadrant, using integration.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y = 5x + 7, x = 2, x = 8
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines:
y = x2 + 1, x = 0, x = 3
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
State whether the following is True or False :
The area bounded by the two cures y = f(x), y = g (x) and X-axis is `|int_"a"^"b" f(x)*dx - int_"b"^"a" "g"(x)*dx|`.
Solve the following :
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
State whether the following statement is True or False:
The area of portion lying below the X axis is negative
The area of the region bounded by the curve y2 = x and the Y axis in the first quadrant and lines y = 3 and y = 9 is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find the area of the region bounded by the curve y = (x2 + 2)2, the X-axis and the lines x = 1 and x = 3
Find area of the region bounded by 2x + 4y = 10, y = 2 and y = 4 and the Y-axis lying in the first quadrant
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
The area of the region bounded by the X-axis and the curves defined by y = cot x, `(pi/6 ≤ x ≤ pi/4)` is ______.
The area of the region bounded by the curve y = sin x and the x-axis in [–π, π] is ______.
If area of the region bounded by y ≥ cot( cot–1|In|e|x|) and x2 + y2 – 6 |x| – 6|y| + 9 ≤ 0, is λπ, then λ is ______.
The area bounded by the x-axis and the curve y = 4x – x2 – 3 is ______.
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
The area bounded by the curve `y = 3/2sqrtx`, the line x = 1 and x-axis is ______ sq. units.
Which integral gives the area bounded by \[x=g(y)\], the \[y\]-axis, and the horizontal lines \[y=c\] and \[y=d\]?
