Advertisements
Advertisements
प्रश्न
The speed of sound as measured by a student in the laboratory on a winter day is 340 m s−1 when the room temperature is C17°. What speed will be measured by another student repeating the experiment on a day when the room temperature is 32°C?
उत्तर
Given:
Velocity of sound v1 = 340 m/s
Temperature T1 = 17°C = 17 + 273 = 290 K
Let the velocity of sound at a temperature T2 be v2.
T2 = 32°C = 273 + 32 = 305 K
Relation between velocity and temperature:
\[v \propto \sqrt{T}\]
\[So, \]
\[\frac{v_1}{v_2} = \frac{\sqrt{T_1}}{\sqrt{T_2}}\]
\[ \Rightarrow v_2 = \frac{\sqrt{v_1} \times \sqrt{T_2}}{\sqrt{T_1}}\]
\[\text { On substituting the respective values, we get: }\]
\[ v_2 = 340 \times \sqrt{\frac{305}{290}} = 349 \text { m/s }\]
Hence, the final velocity of sound is 349 m/s.
APPEARS IN
संबंधित प्रश्न
A cork floating in a calm pond executes simple harmonic motion of frequency
\[\nu\] when a wave generated by a boat passes by it. The frequency of the wave is
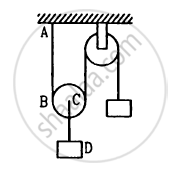
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
The fundamental frequency of a string is proportional to
In a stationary wave,
(a) all the particles of the medium vibrate in phase
(b) all the antinodes vibrates in phase
(c) the alternate antinodes vibrate in phase
(d) all the particles between consecutive nodes vibrate in phase.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
The speed of sound in a medium depends on
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
