Advertisements
Advertisements
प्रश्न
The weather report reads, "Temperature 20°C : Relative humidity 100%". What is the dew point?
उत्तर
Here,
Relative humidity = 100%
RH = `"Vapour pressure of air"/"SVP at the same temperature"` = 1
⇒ Vapour pressure of air = SVP at the same temperature
So , the air is saturated at `20^circ`C . So , dew point is `20^circ` C .
APPEARS IN
संबंधित प्रश्न
Can we define the temperature of (a) vacuum, (b) a single molecule?
Consider a gas of neutrons. Do you expect it to behave much better as an ideal gas as compared to hydrogen gas at the same pressure and temperature?
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
The condition of air in a closed room is described as follows. Temperature = 25°C, relative humidity = 60%, pressure = 104 kPa. If all the water vapour is removed from the room without changing the temperature, what will be the new pressure? The saturation vapour pressure at 25°C − 3.2 kPa.
The temperature and the dew point in an open room are 20°C and 10°C. If the room temperature drops to 15°C, what will be the new dew point?
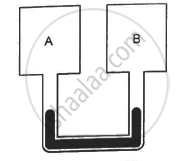
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1m-2. What is the amount of heat radiated by the spherical surface in 20 seconds?
The power radiated by a perfect blackbody depends only on its ______
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
The average translational kinetic energy of gas molecules depends on ____________.
An inflated rubber balloon contains one mole of an ideal gas, has a pressure p, volume V and temperature T. If the temperature rises to 1.1 T, and the volume is increased to 1.05 V, the final pressure will be ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
When the temperature of an ideal gas is increased from 27°C to 227°C, its speed is changed from 400 ms-1 to vs, and Then vs is ______.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
