Advertisements
Advertisements
प्रश्न
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
उत्तर
Given: P = 1.013 × 105 N/m2, V = 5 litres = 5 × 10-3 m3
E = `3/2"PV"`
`= 3/2(1.013xx10^5 "N"/"m"^2)(5xx10^-3 "m"^3)`
= 7.5 × 1.013 × 102 J
= 7.597 × 102 J
This is the required energy.
APPEARS IN
संबंधित प्रश्न
Comment on the following statement: the temperature of all the molecules in a sample of a gas is the same.
Consider a gas of neutrons. Do you expect it to behave much better as an ideal gas as compared to hydrogen gas at the same pressure and temperature?
It is said that the assumptions of kinetic theory are good for gases having low densities. Suppose a container is so evacuated that only one molecule is left in it. Which of the assumptions of kinetic theory will not be valid for such a situation? Can we assign a temperature to this gas?
Is it possible to boil water at room temperature, say 30°C? If we touch a flask containing water boiling at this temperature, will it be hot?
Which of the following parameters is the same for molecules of all gases at a given temperature?
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
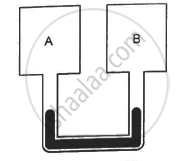
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
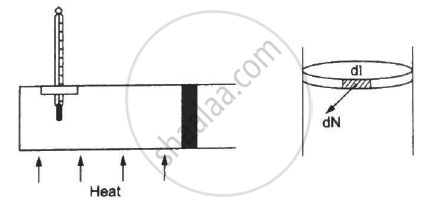
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
Above what temperature, all bodies radiate electromagnetic radiation?
What is the microscopic origin of temperature?
Explain in detail the kinetic interpretation of temperature.
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
Assuming the expression for the pressure exerted by the gas on the wall of the container, it can be shown that pressure is ______.
The average translational kinetic energy of a molecule in a gas is 'E1'. The kinetic energy of the electron (e) accelerated from rest through p.d. 'V' volt is 'E2'. The temperature at which E1 = E2 is possible, is ______.
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of rms speeds.
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
If a = 0. 72 and t = 0.04, then the value of r is ______.
If a = 0. 72 and r = 0.24, then the value of t is ______.
2000 calories of radiant heat is incident on a body. If the body absorbs 550 calories of heat, find the coefficient of emmission of the body.
