Advertisements
Advertisements
प्रश्न
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
उत्तर
Data: T = 280 K, Wien's constant b = 2.897 × 10−3 m K
λmax T = b
∴ `lambda_"max" = "b"/"T"`
= `(2.897 xx 10^-3 "m.K")/(280 "K")`
= 1.035 × 10−5 m
This value lies in the infrared region of the electromagnetic spectrum.
The nature of the curve of blackbody radiation will be the same, but the maximum will occur at 1.035 × 10-5 m.
APPEARS IN
संबंधित प्रश्न
Comment on the following statement: the temperature of all the molecules in a sample of a gas is the same.
Is it possible to boil water at room temperature, say 30°C? If we touch a flask containing water boiling at this temperature, will it be hot?
When you come out of a river after a dip, you feel cold. Explain.
The pressure of an ideal gas is written as \[P = \frac{2E}{3V}\] . Here E refers to
The mean square speed of the molecules of a gas at absolute temperature T is proportional to
The process on an ideal gas, shown in figure, is
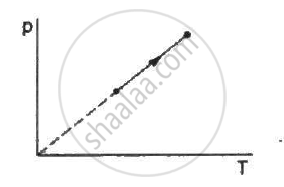
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300 K and that the air behaves as an ideal gas.
Use R = 8.3 J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
Figure shows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0 and its pressure is p0 which equals the atmospheric pressure. (a) What is the tension in the wire? (b) What will be the tension if the temperature is increased to 2T0 ?

The condition of air in a closed room is described as follows. Temperature = 25°C, relative humidity = 60%, pressure = 104 kPa. If all the water vapour is removed from the room without changing the temperature, what will be the new pressure? The saturation vapour pressure at 25°C − 3.2 kPa.
A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
If a = 0.72 and r = 0.24, then the value of tr is ______.
Calculate the ratio of the mean square speeds of molecules of a gas at 30 K and 120 K.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1m-2. What is the amount of heat radiated by the spherical surface in 20 seconds?
Calculate the value of λmax for radiation from a body having a surface temperature of 3000 K. (b = 2.897 x 10-3 m K)
Under which condition laws of Boyle, Charles, and Gay-Lussac are valid?
Explain in detail the kinetic interpretation of temperature.
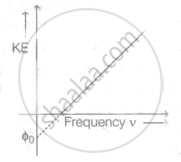
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity `omega`. Its kinetic energy is ______.
The average translational kinetic energy of a molecule in a gas becomes equal to 0.49 eV at a temperature about (Boltzmann constant = 1.38 x 10-23 JK-1) ____________.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
If a = 0. 72 and r = 0.24, then the value of t is ______.
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
