Advertisements
Advertisements
प्रश्न
Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300 K and that the air behaves as an ideal gas.
Use R = 8.3 J K-1 mol-1
उत्तर
Here,
P1 = 2 × 105 pa
V1 = 0.002 m3
V2 = 0.0005 m3
T1 = T2 = 300 K
Number of moles initially , n1 = \[\frac{P_1 V_1}{R T_1} \]
⇒ n1 = \[\frac{2 × {10}^5 \times 0.002}{8.3 × 300} \]
⇒ n1 = 0.16
Applying equation of state, we get
P2 V2 = n2 RT
Assuming the final pressure becomes equal to the atmospheric pressure, we get
P2 = 1.0 × 105 pa
⇒ n2 = \[\frac{P_2 V_2}{RT} \]
⇒ n2 = \[\frac{1.0 × {10}^5 × 0.0005}{8.3 × 300} \]
⇒ n2 = 0.02
Number of leaked moles= n2 - n1
= 0.16 -0.02
= 0.14
APPEARS IN
संबंधित प्रश्न
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?
Use R = 8.314 JK-1 mol-1
0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1
During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
The condition of air in a closed room is described as follows. Temperature = 25°C, relative humidity = 60%, pressure = 104 kPa. If all the water vapour is removed from the room without changing the temperature, what will be the new pressure? The saturation vapour pressure at 25°C − 3.2 kPa.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
In an ideal gas, the molecules possess
When a gas is heated, its temperature increases. Explain this phenomenon on the basis of the kinetic theory of gases.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Why the temperature of all bodies remains constant at room temperature?
Above what temperature, all bodies radiate electromagnetic radiation?
If the density of nitrogen is 1.25 kg/m3 at a pressure of 105 Pa, find the root mean square velocity of nitrogen molecules.
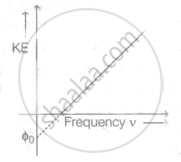
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
Which of the following materials is diathermanous?
