Advertisements
Advertisements
प्रश्न
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
उत्तर
Mean velocity is given by \[V_{avg} = \sqrt{\frac{8RT}{\pi M}}\]
Let temperature for H and He respectively be T1 and T2, respectively.
For hydrogen:
MH = 2g = 2 \[\times\] 10-3 kg
For helium:
MHe= 4 g = 4 \[\times\] 10-3 kg
Now,
A/q \[\sqrt{\frac{8R T_1}{\pi M_H}} = \sqrt{\frac{8R T_2}{\pi M_{He}}}\]
\[ \Rightarrow \sqrt{\frac{8R T_1}{2 \times {10}^{- 3} \pi}} = \sqrt{\frac{8R T_2}{\pi \times 4 \times {10}^{- 3}}}\]
\[ \Rightarrow \sqrt{\frac{T_1}{2}} = \sqrt{\frac{T_2}{4}}\]
\[ \Rightarrow \frac{T_1}{T_2} = \frac{1}{2}\]
\[ \Rightarrow T_1 : T_2 = 1: 2\]
APPEARS IN
संबंधित प्रश्न
Comment on the following statement: the temperature of all the molecules in a sample of a gas is the same.
Consider a gas of neutrons. Do you expect it to behave much better as an ideal gas as compared to hydrogen gas at the same pressure and temperature?
The mean square speed of the molecules of a gas at absolute temperature T is proportional to
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.

An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
Explain, on the basis of the kinetic theory of gases, how the pressure of a gas changes if its volume is reduced at a constant temperature.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1m-2. What is the amount of heat radiated by the spherical surface in 20 seconds?
Why the temperature of all bodies remains constant at room temperature?
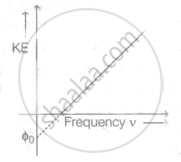
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
The average translational kinetic energy of a molecule in a gas becomes equal to 0.49 eV at a temperature about (Boltzmann constant = 1.38 x 10-23 JK-1) ____________.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of average K.E.
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of rms speeds.
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
At what temperature will therms velocity of a gas be four times its value at STP?
