Advertisements
Advertisements
प्रश्न
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
उत्तर
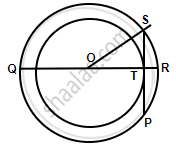
OS = 5 cm
OT = 3 cm
In Rt. Triangle OST
By Pythagoras Theorem,
ST2 = OS2 – OT2
ST2 = 25 – 9
ST2 = 16
ST = 4 cm
Since OT is perpendicular to SP and OT bisects chord SP
So, SP = 8 cm
APPEARS IN
संबंधित प्रश्न
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centres if:
- they touch each other externally,
- they touch each other internally.
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
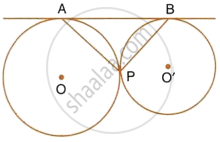
- tangent at point P bisects AB,
- angles APB = 90°.
Two circle with centres O and O' are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. Prove that OA bisects angle BAC.

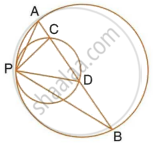
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that ∠CPA = ∠DPB.
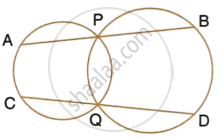
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.
Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T; show that the points P, B, Q and T are concyclic.
Two circles intersect each other at points A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
In the figure, given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
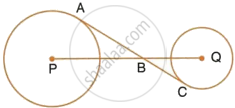
Given that AB = 8 cm, calculate PQ.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if -
they touch each other internally.
P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.
