Advertisements
Advertisements
प्रश्न
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
उत्तर
Radius of coil X, r1 = 16 cm = 0.16 m
Radius of coil Y, r2 = 10 cm = 0.1 m
Number of turns of on coil X, n1 = 20
Number of turns of on coil Y, n2 = 25
Current in coil X, I1 = 16 A
Current in coil Y, I2 = 18 A
Magnetic field due to coil X at their centre is given by the relation,
`"B"_1 = (mu_0"n"_1"I"_1)/(2"r"_1)`
Where,
`mu_0` = Permeability of free space = 4π × 10−7 T mA−1
∴ `"B"_1 = (4pi xx 10^-7 xx 20 xx 16)/(2 xx 0.16)`
= 4π × 10−4 T .........(towards East)
Magnetic field due to coil Y at their centre is given by the relation,
`"B"_2 = (mu_0"n"_2"I"_2)/(2"r"_2)`
= `(4pi xx 10^-7 xx 25 xx 18)/(2 xx 0.10)`
= 9π × 10−4 T .........(towards West)
Hence, net magnetic field can be obtained as:
`"B" = "B"_2 - "B"_1`
= 9π × 10−4 − 4π × 10−4
= 5π × 10−4 T
= 1.57 × 10−3 T ........(towards West)
APPEARS IN
संबंधित प्रश्न
At a place, the horizontal component of earth's magnetic field is B and angle of dip is 60°. What is the value of horizontal component of the earth's magnetic field at equator?
Use Biot-Savart's law to find the expression for the magnetic field due to a circular loop of radius 'r' carrying current 'I', at its centre ?
A current-carrying, straight wire is kept along the axis of a circular loop carrying a current. This straight wire
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.
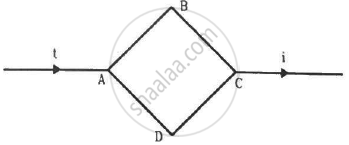
Figure shows a square loop ABCD with edge-length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.
A circular loop of radius 20 cm carries a current of 10 A. An electron crosses the plane of the loop with a speed of 2.0 × 106 m s−1. The direction of motion makes an angle of 30° with the axis of the circle and passes through its centre. Find the magnitude of the magnetic force on the electron at the instant it crosses the plane.
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
A charge of 3.14 × 10−6 C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s−1. Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
Which of these equations is the correct expression for force on a charge in magnetic field?
The magnitude of the magnetic field due to a circular coil of radius R carrying a current I at an axial distance x from the centre is ______.
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
If we double the radius of a coil keeping the current through it unchanged, then the magnetic field at any point at a large distance from the centre becomes approximately.
A short bar magnet has a magnetic moment of 0. 65 J T-1, then the magnitude and direction of the magnetic field produced by the magnet at a distance 8 cm from the centre of magnet on the axis is ______.
A small square loop of wire of side l is placed inside a large square loop of side L (L >> l). The loop is coplanar and their centers coincide. The mutual inductance of the system is proportional to is
Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral
`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.
- Show that ℑ(L) monotonically increases with L.
- Use an appropriate Amperian loop to show that ℑ(∞) = µ0I, where I is the current in the wire.
- Verify directly the above result.
- Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?
The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.
(Take r < a).
