Advertisements
Advertisements
प्रश्न
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC and measure its radius.
उत्तर
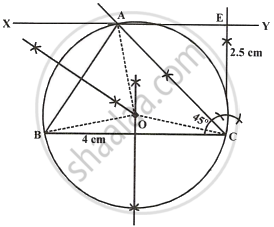
Steps of construction:
- Draw a line segment BC = 4 cm.
- At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm.
- From E, draw another perpendicular line EY.
- From C, draw a ray making an angle of 45° with CB, which intersects EY at A.
- Join AB.
- ΔABC is the required triangle.
- Draw perpendicular bisectors of sides AB and BC intersecting each other at O.
- With centre O, and radius OB, draw a circle which will pass through A, B and C.
Measuring the radius OB = OC = OA = 2 cm.
APPEARS IN
संबंधित प्रश्न
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q. Give the justification of the construction.
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
