Question

वक्रों y² = 4x एवं y = 2x के मध्यवर्ती क्षेत्र का क्षेत्रफल है:

पर्याय

• `2/3`

• `1/3`

• `1/4`

• `3/4`

Answer 1

`1/3`

स्पष्टीकरण:

वक्र का समीकरण y² = 4x   …(i)

रेखा का समीकरण y = 2x    …(ii)

समीकरण (i) व (ii) से

(2x)² = 4x

4x² = 4x

⇒ x² - x = 0

⇒ x(x - 1) = 0

⇒ x = 0, x = 1

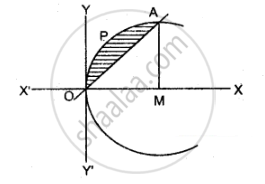
समीकरण (ii) से जब x = 0, y= 0 और जब x = 1, y = 2

समीकरण (i) व समीकरण (ii) का प्रतिच्छेदन बिंदु (0, 0) तथा A(1, 2) हैं।

अभीष्ट क्षेत्रफल

`= int_0^1  "y  dx"  "(वक्र के लिए)" - int_0^1 "y  dx"` (रेखा के लिए)

`int_0^1 2 sqrt x  "dx" - int_0^1  2x  "dx"`

`= 2 xx 2/3  [x^(3//2)]_0^1 - 2 [x^2/2]_0^1`

`= 4/3 [1 - 0] - [1 - 0]`

`= 4/3 - 1`

`= 1/3`  वर्ग इकाई