Advertisements
Advertisements
प्रश्न
वृत्त x2 + y2 = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
पर्याय
2π वर्ग इकाई
π वर्ग इकाई
3π वर्ग इकाई
4π वर्ग इकाई
उत्तर
सही उत्तर π वर्ग इकाई है।
व्याख्या:
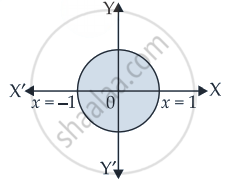
वृत्त का समीकरण दिया गया है x2 + y2 = 1
⇒ y = `sqrt(1 - x^2)`
क्योंकि वृत्त अक्षों के परितः सममित है।
∴ वाँछित क्षेत्रफल = `4 xx int_0^1 sqrt(1 - x^2) "d"x`
= `4[x/2 sqrt(1 - x^2) + 1/2 sin^-1 x]_0^1`
= `4[0 + 1/2 sin^-1 (1) - 0 - 0]`
= `4 xx 1/2 xx pi/2`
= π वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
समाकलन विधि का उपयोग करते हुए वक्र |x| + |y| = 1से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन विधि का उपयोग करते हुए, रेखाओं 2x + y = 4, 3x – 2y = 6 एवं x – 3y + 5 = 0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
0 और π के बीच, वक्र y = sin x का क्षेत्रफल ज्ञात कीजिए।

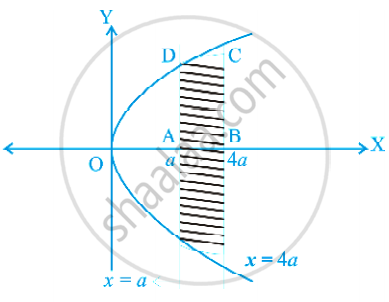
वक्र x = at2 और y = 2at द्वारा t = 1 और t = 2 के संगत कोटियों के बीच परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वृत्त x2 + y2 = 2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
वक्र x = y2 , y-अक्ष तथा रेखा y = 3 और y = 4 से परिबद्ध क्षेत्र का क्षेत्रफल ______ है।
वक्र y2 = 9x, और y = 3x से परिबद्ध क्षेत्रफल का क्षेत्रफल ज्ञात कीजिए।
परवलय y2 = 2px, और x2 = 2py से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = x3 , y = x + 6 और x = 0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 4x और x2 = 4y से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y2 = 9x और y = x बीच में पड़ने वाले क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय x2 = y और रेखा y = x + 2 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
क्षेत्र `{(x, 0) : y = sqrt(4 - x^2)}` और x-अक्ष का चित्रण कीजिए। समाकलन का उपयोग करते हुए इस क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = `sqrt("a"^2 - x^2)` के अंतर्गत तथा x = 0 और x = a रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y = `sqrtx` और y = x से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = –x2 और सरल रेखा x + y + 2 = 0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 2x और x2 + y2 = 4x से परिंबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन का प्रयोग करते हुए, उस त्रिभुज द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जिसके शीर्ष (-1, 1), (0, 5) और (3, 2) हैं।
रेखा x + 2y = 2, y – x = 1 और 2x + y = 7 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y-अक्ष, y = cosx, y = sinx, 0 ≤ x ≤ `pi/2` से परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र x2 = 4y और सरल रेखा x = 4y – 2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = `sqrt(16 - x^2)` और x-अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = x + 1 तथा x = 2 और x = 3 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
