Advertisements
Advertisements
प्रश्न
Water is dripping out at a steady rate of 1 cu cm/sec through a tiny hole at the vertex of the conical vessel, whose axis is vertical. When the slant height of water in the vessel is 4 cm, find the rate of decrease of slant height, where the vertical angle of the conical vessel is `pi/6`
उत्तर
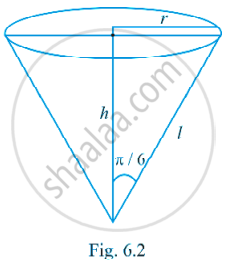
Given that `"dv"/"dt"` = 1 cm3/s
Where v is the volume of water in the conical vessel.
From the Fig.6.2, l = 4 cm
h = `"l" cos pi/6`
= `sqrt(3)/2 "l"` and r = `"l" sin pi/6 = "l"/2`.
Therefore, v = `1/3 pi"r"^2"h"`
= `pi/3 "l"^2/4 sqrt(3)/2 "l"`
= `(sqrt(3)pi)/24 "l"^3`
`"dv"/"dt" = (sqrt(3)pi)/8 "l"^2 "dl"/"dt"`
Therefore, l = `(sqrt(3)pi)/8 16 * "dl"/"dt"`
⇒ `"dl"/"dt" = 1/(2sqrt(3)pi)` cm/s.
Therefore, the rate of decrease of slant height = `1/(2sqrt(3)pi)` cm/s
APPEARS IN
संबंधित प्रश्न
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
The side of a square sheet is increasing at the rate of 4 cm per minute. At what rate is the area increasing when the side is 8 cm long?
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
Find an angle θ whose rate of increase twice is twice the rate of decrease of its cosine ?
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
If \[V = \frac{4}{3}\pi r^3\] , at what rate in cubic units is V increasing when r = 10 and \[\frac{dr}{dt} = 0 . 01\] ? _________________
A cone whose height is always equal to its diameter is increasing in volume at the rate of 40 cm3/sec. At what rate is the radius increasing when its circular base area is 1 m2?
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
For what values of x is the rate of increase of x3 − 5x2 + 5x + 8 is twice the rate of increase of x ?
The coordinates of the point on the ellipse 16x2 + 9y2 = 400 where the ordinate decreases at the same rate at which the abscissa increases, are
The volume of a sphere is increasing at 3 cm3/sec. The rate at which the radius increases when radius is 2 cm, is
If the rate of change of volume of a sphere is equal to the rate of change of its radius, then its radius is equal to
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
In a sphere the rate of change of volume is
In a sphere the rate of change of surface area is
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
A particle is moving along the curve x = at2 + bt + c. If ac = b2, then particle would be moving with uniform ____________.
If the rate of change of volume of a sphere is equal to the rate of change of its radius then the surface area of a sphere is ____________.
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
