Advertisements
Advertisements
Question
Water is dripping out at a steady rate of 1 cu cm/sec through a tiny hole at the vertex of the conical vessel, whose axis is vertical. When the slant height of water in the vessel is 4 cm, find the rate of decrease of slant height, where the vertical angle of the conical vessel is `pi/6`
Solution
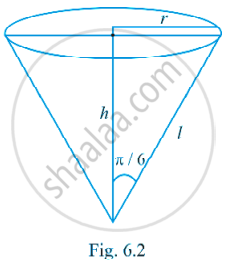
Given that `"dv"/"dt"` = 1 cm3/s
Where v is the volume of water in the conical vessel.
From the Fig.6.2, l = 4 cm
h = `"l" cos pi/6`
= `sqrt(3)/2 "l"` and r = `"l" sin pi/6 = "l"/2`.
Therefore, v = `1/3 pi"r"^2"h"`
= `pi/3 "l"^2/4 sqrt(3)/2 "l"`
= `(sqrt(3)pi)/24 "l"^3`
`"dv"/"dt" = (sqrt(3)pi)/8 "l"^2 "dl"/"dt"`
Therefore, l = `(sqrt(3)pi)/8 16 * "dl"/"dt"`
⇒ `"dl"/"dt" = 1/(2sqrt(3)pi)` cm/s.
Therefore, the rate of decrease of slant height = `1/(2sqrt(3)pi)` cm/s
APPEARS IN
RELATED QUESTIONS
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
A balloon, which always remains spherical, has a variable diameter `3/2 (2x + 1)` Find the rate of change of its volume with respect to x.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
The total revenue received from the sale of x units of a product is given by R (x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7 ?
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
The surface area of a spherical bubble is increasing at the rate of 2 cm2/s. When the radius of the bubble is 6 cm, at what rate is the volume of the bubble increasing?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
The side of an equilateral triangle is increasing at the rate of \[\frac{1}{3}\] cm/sec. Find the rate of increase of its perimeter ?
If the rate of change of volume of a sphere is equal to the rate of change of its radius, find the radius of the sphere ?
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
The distance moved by the particle in time t is given by x = t3 − 12t2 + 6t + 8. At the instant when its acceleration is zero, the velocity is
The radius of a circular plate is increasing at the rate of 0.01 cm/sec. The rate of increase of its area when the radius is 12 cm, is
In a sphere the rate of change of volume is
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
Let y = f(x) be a function. If the change in one quantity 'y’ varies with another quantity x, then which of the following denote the rate of change of y with respect to x.
What is the rate of change of the area of a circle with respect to its radius when, r = 3 cm
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is ______.
If the circumference of circle is increasing at the constant rate, prove that rate of change of area of circle is directly proportional to its radius.
