Question

Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.

Answer 1

\[\text{ Let r be the radius, h be the height and V be the volume of the cone at any time t } .\]

\[\text { Then }, \]
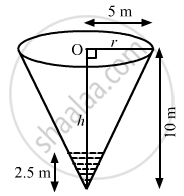
\[V=\frac{1}{3}\pi r^2 h\]
\[ \Rightarrow \frac{dV}{dt} = \frac{1}{3}\pi r^2 \frac{dh}{dt}+\frac{2}{3}\pi r h\frac{dr}{dt}\]
\[\text { Now,}\]
\[\frac{h}{r}=\frac{10}{5}\text{or r}=\frac{h}{2}\text { and }\frac{dh}{dt}=2\frac{dr}{dt}\]
\[\Rightarrow\frac{dV}{dt} = \frac{1}{3}\pi \left( \frac{h}{2} \right)^2 \frac{dh}{dt}+\frac{2}{3}\pi\left( \frac{h}{2} \right)h\frac{1}{2}\frac{dh}{dt}\]
\[\Rightarrow\frac{dV}{dt} = \frac{\pi}{3}\left[ \frac{h^2}{4}\frac{dh}{dt}+\frac{h^2}{2}\frac{dh}{dt} \right]\]
\[\Rightarrow\frac{dV}{dt}=\frac{\pi}{3}\times\frac{3 h^2 dh}{4dt}\]
\[\Rightarrow\frac{dV}{dt}=\frac{\pi h^2}{4}\frac{dh}{dt}\]
\[ \Rightarrow \frac{\pi h^2}{4}\frac{dh}{dt} = \pi\]
\[ \Rightarrow \frac{dh}{dt} = \frac{4}{h^2}\]
\[ \Rightarrow \frac{dh}{dt} = \frac{4}{\left( 2 . 5 \right)^2}\]
\[ \Rightarrow \frac{dh}{dt} = \text{0 . 64 m}/\min\]