Question

A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of

पर्याय

• 15 ft/sec

• 9 ft/sec

•  6 ft/sec

• none of these

Answer 1

 6 ft/sec
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y ft be the length of his shadow CE.

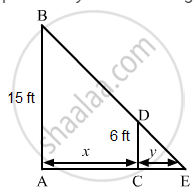
\[\text { Since the triangles ABE and CDE are similar }, \]

\[\frac{AB}{CD} = \frac{AE}{CE}\]

\[\Rightarrow \frac{15}{6} = \frac{x + y}{y}\]

\[ \Rightarrow \frac{x}{y} = \frac{15}{6} - 1\]

\[ \Rightarrow \frac{x}{y} = \frac{3}{2}\]

\[ \Rightarrow y = \frac{2}{3}x\]

\[ \Rightarrow \frac{dy}{dt} = \frac{2}{3}\left( \frac{dx}{dt} \right)\]

\[ \Rightarrow \frac{dy}{dt} = \frac{2}{3} \times 9\]

\[ \Rightarrow \frac{dy}{dt} = 6 \text { ft }/\sec\]