Advertisements
Advertisements
प्रश्न
We would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If αiron = 1.2 × 10−5/K and αbrass = 1.8 × 10−5/K, what should we take as length of each strip?
Advertisements
उत्तर
According to the problem, L1 – Lb = 10 cm where,
L1 = length of iron scale
Lb = Length of brass scale
This condition is possible if the change in length of both rods is remain the same at all temperatures.
Change in length of iron rod,
`ΔL = α_IL_IΔT`
Change in length of brass rod,
`ΔL = α_BL_BΔT`
As the change will equal in both the rods, so
`α_IL_IΔT = α_BL_BΔT`
⇒ `α_IL_I = α_BL_B`
⇒ `L_I/L_B = α_B/α_I`
Here, `α_B = 1.8 xx 10^-5 K^-1, α_I = 1.2 xx 10^-5 K^-1`
∴ `L_I/L_B = (1.8 xx 10^-5)/(1.2 xx 10^-5) = 3/2`
`L_I = 3/2 L_B`
As, `L_I - L_B` = 10 cm
∴ `3/2 L_B - L_B` = 10
⇒ `1/2 L_B` = 10
⇒ LB = 20 cm.
APPEARS IN
संबंधित प्रश्न
Explain why a brass tumbler feels much colder than a wooden tray on a chilly day
A tightly closed metal lid of a glass bottle can be opened more easily if it is put in hot water for some time. Explain.
Find the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are 12 × 10–6 °C–1 and 23 × 10–6 °C–1 respectively.
A glass window is to be fit in an aluminium frame. The temperature on the working day is 40°C and the glass window measures exactly 20 cm × 30 cm. What should be the size of the aluminium frame so that there is no stress on the glass in winter even if the temperature drops to 0°C? Coefficients of linear expansion for glass and aluminium are 9.0 × 10–6 °C–1 and 24 ×100–6°C–1 , respectively.
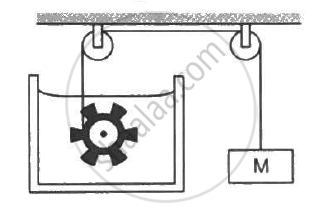
Following Figure shows water in a container having 2.0 mm thick walls made of a material of thermal conductivity 0.50 W m−1°C−1. The container is kept in a melting-ice bath at 0°C. The total surface area in contact with water is 0.05 m2. A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10 cm s−1 and the temperature of the water remains constant at 1.0°C. Find the mass M of the block. Assume that the heat flows out of the water only through the walls in contact. Take g = 10 m s−2.
On a winter day when the atmospheric temperature drops to −10°C, ice forms on the surface of a lake. (a) Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed. (b) Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m−3, latent heat of fusion of ice = 3.36 × 105 J kg−1and thermal conductivity of ice = 1.7 W m−1°C−1. Neglect the expansion of water of freezing.
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.
Consider the situation shown in the figure . The frame is made of the same material and has a uniform cross-sectional area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100°C is 130 J.
A room has a window fitted with a single 1.0 m × 2.0 m glass of thickness 2 mm. (a) Calculate the rate of heat flow through the closed window when the temperature inside the room is 32°C and the outside is 40°C. (b) The glass is now replaced by two glasspanes, each having a thickness of 1 mm and separated by a distance of 1 mm. Calculate the rate of heat flow under the same conditions of temperature. Thermal conductivity of window glass = 1.0 J s−1 m−1°C−1 and that of air = 0.025 m-1°C-1 .
Four identical rods AB, CD, CF and DE are joined as shown in following figure . The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
Following figure shows two adiabatic vessels, each containing a mass m of water at different temperatures. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperatures in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.
The coefficient of thermal conductivity depends upon ______.
Heat is associated with ______.
These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
As per the given figure, two plates A and B of thermal conductivity K and 2 K are joined together to form a compound plate. The thickness of plates are 4.0 cm and 2.5 cm respectively and the area of cross-section is 120 cm2 for each plate. The equivalent thermal conductivity of the compound plate is `(1+5/alpha)`K, then the value of a will be ______.
Which of the following is a correct example of a bad conductor of heat used in daily life to reduce heat loss or gain?
At the molecular level, how is heat transferred in a solid during conduction?
