Advertisements
Advertisements
प्रश्न
What should be subtracted to the polynomial x2 − 16x + 30, so that 15 is the zero of the resulting polynomial?
पर्याय
30
14
15
16
उत्तर
We know that, if `x = alpha`, is zero of a polynomial then `x-alpha` is a factor of f(x)
Since 15 is zero of the polynomial f (x) = x2 − 16x + 30, therefore (x − 15) is a factor of f (x)
Now, we divide f(x) = x2 − 16x + 30 by ( x - 15) we get
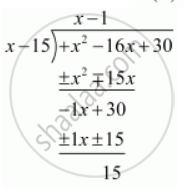
Thus we should subtract the remainder 15 from `x^2 - 16x+30`
Hence, the correct choice is (c).
APPEARS IN
संबंधित प्रश्न
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients.
4u2 + 8u
If α and β are the zeros of the quadratic polynomial f(x) = x2 − px + q, prove that `alpha^2/beta^2+beta^2/alpha^2=p^4/q^2-(4p^2)/q+2`
If α and β are the zeroes of the polynomial f(x) = x2 + px + q, form a polynomial whose zeroes are (α + β)2 and (α − β)2.
If the zeros of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are in A.P., prove that 2b3 − 3abc + a2d = 0.
Find the zeroes of the quadratic polynomial `(8x^2 ˗ 4)` and verify the relation between the zeroes and the coefficients
If (x+a) is a factor of the polynomial `2x^2 + 2ax + 5x + 10`, find the value of a.
If two zeros x3 + x2 − 5x − 5 are \[\sqrt{5}\ \text{and} - \sqrt{5}\], then its third zero is
If 2 and `1/2` are the zeros of px2 + 5x + r, then ______.
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If the sum of the roots is –p and the product of the roots is `-1/"p"`, then the quadratic polynomial is:
The zeroes of the quadratic polynomial x2 + 99x + 127 are ______.
