Advertisements
Advertisements
Question
What should be subtracted to the polynomial x2 − 16x + 30, so that 15 is the zero of the resulting polynomial?
Options
30
14
15
16
Solution
We know that, if `x = alpha`, is zero of a polynomial then `x-alpha` is a factor of f(x)
Since 15 is zero of the polynomial f (x) = x2 − 16x + 30, therefore (x − 15) is a factor of f (x)
Now, we divide f(x) = x2 − 16x + 30 by ( x - 15) we get
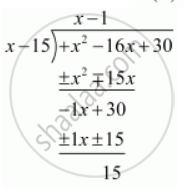
Thus we should subtract the remainder 15 from `x^2 - 16x+30`
Hence, the correct choice is (c).
APPEARS IN
RELATED QUESTIONS
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients.
6x2 – 3 – 7x
If a and 3 are the zeros of the quadratic polynomial f(x) = x2 + x − 2, find the value of `1/alpha-1/beta`.
If 𝛼 and 𝛽 are the zeros of the quadratic polynomial f(t) = t2 − 4t + 3, find the value of `alpha^4beta^3+alpha^3beta^4`
If α and β are the zeros of a quadratic polynomial such that α + β = 24 and α − β = 8, find a quadratic polynomial having α and β as its zeros.
If α and β are the zeros of the quadratic polynomial f(x) = x2 − p (x + 1) — c, show that (α + 1)(β +1) = 1− c.
Find the quadratic polynomial, sum of whose zeroes is `( 5/2 )` and their product is 1. Hence, find the zeroes of the polynomial.
On dividing `3x^3 + x^2 + 2x + 5` is divided by a polynomial g(x), the quotient and remainder are (3x – 5) and (9x + 10) respectively. Find g(x).
A quadratic polynomial, whose zeroes are –3 and 4, is ______.
If one of the zeroes of the cubic polynomial x3 + ax2 + bx + c is –1, then the product of the other two zeroes is ______.
Given that the zeroes of the cubic polynomial x3 – 6x2 + 3x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
