Advertisements
Advertisements
Question
What should be added to the polynomial x2 − 5x + 4, so that 3 is the zero of the resulting polynomial?
Options
1
2
4
5
Solution
If `x = alpha`, is a zero of a polynomial then `x -alpha `is a factor of `f(x)`
Since 3 is the zero of the polynomial , f(x) = x2 − 5x + 4,
Therefore `x - 3`is a factor of `f(x)`
Now, we divide`f(x) = x^2 - 5x + 4 ` by `(x - 3)` we get
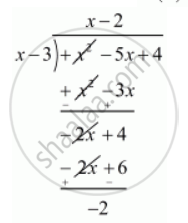
Therefore we should add 2 to the given polynomial
Hence, the correct choice is (b).
APPEARS IN
RELATED QUESTIONS
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients:
4s2 – 4s + 1
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case
x3 – 4x2 + 5x – 2; 2, 1, 1
Find all zeroes of the polynomial `(2x^4 - 9x^3 + 5x^2 + 3x - 1)` if two of its zeroes are `(2 + sqrt3)` and `(2 - sqrt3)`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate `1/alpha+1/beta-2alphabeta`
If two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero, then the third zero is
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If the sum of the roots is –p and the product of the roots is `-1/"p"`, then the quadratic polynomial is:
The number of polynomials having zeroes as –2 and 5 is ______.
Can the quadratic polynomial x2 + kx + k have equal zeroes for some odd integer k > 1?
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
4x2 – 3x – 1
Find a quadratic polynomial whose zeroes are 6 and – 3.
