Advertisements
Advertisements
Question
On dividing `3x^3 + x^2 + 2x + 5` is divided by a polynomial g(x), the quotient and remainder are (3x – 5) and (9x + 10) respectively. Find g(x).
Solution
By using division rule, we have
Dividend = Quotient × Divisor + Remainder
∴` 3x^3 + x^2 + 2x + 5 = (3x – 5)g(x) + 9x + 10`
⇒`3x^3 + x^2 + 2x + 5 – 9x – 10 = (3x – 5)g(x)`
⇒`3x^3 + x^2 – 7x – 5 = (3x – 5)g(x)`
⇒ `(g(x)=3x^3+x^2-7x-5)/(3x-5)`
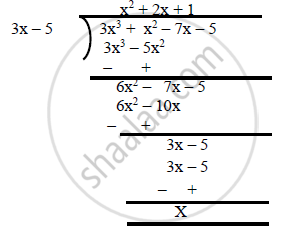
`∴g(x) = x^2 + 2x + 1`
APPEARS IN
RELATED QUESTIONS
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients.
6x2 – 3 – 7x
Find a quadratic polynomial with the given numbers as the sum and product of its zeroes respectively.
`0, sqrt5`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate :
`a(α^2/β+β^2/α)+b(α/β+β/α)`
If α and β are the zeros of the quadratic polynomial f(x) = x2 − px + q, prove that `alpha^2/beta^2+beta^2/alpha^2=p^4/q^2-(4p^2)/q+2`
Find the zeroes of the quadratic polynomial f(x) = 4x2 - 4x - 3 and verify the relation between its zeroes and coefficients.
If f(x) = `x^4– 5x + 6" is divided by g(x) "= 2 – x2`
If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, the\[\frac{1}{\alpha} + \frac{1}{\beta} + \frac{1}{\gamma} =\]
For the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also find the zeroes of these polynomials by factorisation.
`21/8, 5/16`
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
`y^2 + 3/2 sqrt(5)y - 5`
Find the zeroes of the quadratic polynomial 4s2 – 4s + 1 and verify the relationship between the zeroes and the coefficients.
