Advertisements
Advertisements
प्रश्न
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity
उत्तर
Lorentz magnetic force,
Work done due to Lorentz force
=
=
as
Hence, work done by the force on the charged particle will be zero.
APPEARS IN
संबंधित प्रश्न
Write the expression for the force
A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one point. If a magnetic field is switched on in the vertical direction, the tension in the string
If a charged particle moves unaccelerated in a region containing electric and magnetic fields
(a)
(b)
(c) must be perpendicular to v_B
When a proton is released from rest in a room, it starts with an initial acceleration a0towards west. When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the electric field and the maximum possible magnetic field in the room.
A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by an α-particle moving with the same speed in the same magnetic field?
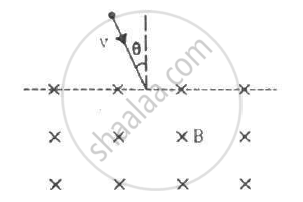
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B, as shown in the figure. (a) Find the radius of the circular arc it describes in the magnetic field. (b) Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.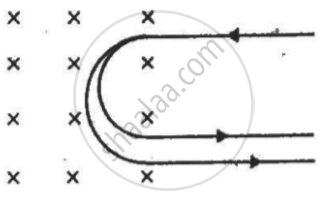
A narrow beam of singly charged potassium ions of kinetic energy 32 keV is injected into a region of width 1.00 cm with a magnetic field of strength 0.500 T, as shown in the figure. The ions are collected at a screen 95.5 cm away from the field region. If the beam contains isotopes of atomic weights 39 and 41, find the separation between the points where these isotopes strike the screen. Take the mass of a potassium ion = A (1.6 × 10−27) kg, where A is the mass number.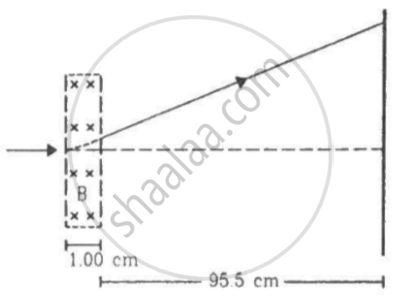
A particle with a charge of 5.0 µC and a mass of 5.0 × 10−12 kg is projected with a speed of 1.0 km s−1 in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field and the velocity is sin−1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.
