SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2024-2025
Date: मार्च 2025
Advertisements
General Instructions :
- All questions are compulsory.
- Use of a calculator is not allowed.
- The numbers to the right of the questions indicate full marks.
- In case of MCQs (Q. No. 1(A)) only the first attempt will be evaluated and will be given credit.
- For every MCQ, the correct alternative (A), (B), (C) or (D) with subquestion number is to be written as an answer.
- Draw proper figures for answers wherever necessary.
- The marks of construction should be clear. Do not erase them.
- Diagram is essential for writing the proof of the theorem.
What is the distance of the point (– 5, 4) from the origin?
3 units
`sqrt(14)` units
`sqrt(31)` units
`sqrt(41)` units
Chapter: [0.05] Co-ordinate Geometry
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
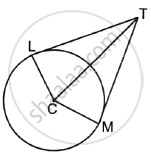
30°
60°
45°
55°
Chapter: [0.03] Circle
What will be the value of sin 45° + `1/sqrt(2)`?
`1 + sqrt(2)`
`2sqrt(2)`
`1/sqrt(2)`
`sqrt(2)`
Chapter: [0.06] Trigonometry
In the right-angled triangle ABC, Hypotenuse AC = 10 and side AB = 5, then what is the measure of ∠A?
30°
60°
90°
45°
Chapter: [0.02] Pythagoras Theorem
What is the name of the point of intersection of coordinate axes?
Chapter: [0.05] Co-ordinate Geometry
Find the value of sin 45° + cos 45° + tan 45°.
Chapter: [0.06] Trigonometry
Chord AB and chord CD of a circle with centre 0 are congruent. If m(arc AB) = 120°, then find the m(arc CD).
Chapter: [0.03] Circle
`square`ABCD is cyclic. If ∠B = 110°, then find measure of ∠D.
Chapter: [0.03] Circle
Advertisements
Prove that, The areas of two triangles with the same height are in proportion to their corresponding bases. To prove this theorem start as follows:
- Draw two triangles, give the names of all points, and show heights.
- Write 'Given' and 'To prove' from the figure drawn.
Chapter: [0.01] Similarity
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
Chapter: [0.05] Co-ordinate Geometry
Two circles with centres O and O' touch each other at point L. Prove that, a tangent through L bisects the common tangent AB of the two circles at point M.
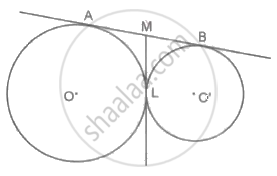
Given: AB is a common tangent of the two circles that touch each other at point L. ML is a tangent through point L.
To prove: M is a mid-point of the tangent AB or MA = MB.
Proof: From the figure,
M is an external point that draws two tangents, MA and ML to the circle with the centre O.
So, `square` = `square` ......(i)
Similarly, M draws two tangents ML and MB to the circle with the centre O'.
So, `square` = `square` ......(ii)
From the equations (i) and (ii),
`square` = `square`
Hence, the tangent at the point L, bisects the common tangent, AB of the two circles at point M.
Chapter: [0.03] Circle
In the figure, the centre of the circle is O and ∠STP = 40°.
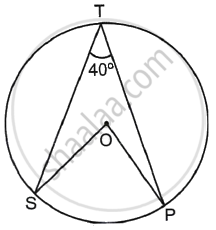
- m (arc SP) = ? By which theorem?
- m ∠SOP = ? Give reason.
Chapter: [0.03] Circle
Find the value of y, if the points A(3, 4), B(6, y) and C(7, 8) are collinear.
Chapter: [0.03] Circle
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
Chapter: [0.02] Pythagoras Theorem
If length of the circular arc is 10 cm and the radius 3·5 cm, find the area of the sector of the circle.
Chapter: [0.07] Mensuration
Draw a circle of radius 4 cm. Draw a point 8 cm away from its centre and construct a pair of tangents.
Chapter: [0.04] Geometric Constructions
Advertisements
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
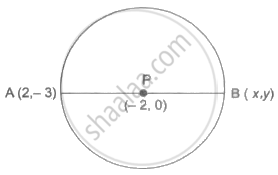
Given: A`square` and P`square`. Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
`square = (square + x)/square`
⇒ `square = square` + x
⇒ x = `square - square`
⇒ x = – 6
and `square = (square + y)/2`
⇒ `square` + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
Chapter: [0.05] Co-ordinate Geometry
Prove that sec θ + tan θ = `cos θ/(1 - sin θ)`.
Proof: L.H.S. = sec θ + tan θ
= `1/square + square/square`
= `square/square` ......`(∵ sec θ = 1/square, tan θ = square/square)`
= `((1 + sin θ) square)/(cos θ square)` ......[Multiplying `square` with the numerator and denominator]
= `(1^2 - square)/(cos θ square)`
= `square/(cos θ square)`
= `cos θ/(1 - sin θ)` = R.H.S.
∴ L.H.S. = R.H.S.
∴ sec θ + tan θ = `cos θ/(1 - sin θ)`
Chapter: [0.06] Trigonometry
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
Chapter: [0.06] Trigonometry
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

Chapter: [0.01] Similarity
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
Chapter: [0.01] Similarity
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Chapter: [0.06] Trigonometry
ΔPQR, is a right angled triangle with ∠Q = 90°, QR = b, and A(ΔPQR) = a. If QN ⊥ PR, then prove that QN = `(2ab)/sqrt(b^4 + 4a^2)`
Chapter: [0.02] Pythagoras Theorem
Use area theorem of similar triangles to prove congruency of two similar triangles with equal areas.
Chapter: [0.01] Similarity
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
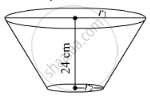
Chapter: [0.07] Mensuration
A person starts his trip from home. He moves 24 km in south direction and then starts moving towards east. He travels 7 km in that direction and finally reaches his destination. How far is the destination from his home?
Chapter: [0.02] Pythagoras Theorem
If m and n are real numbers and m > n, if m2 + n2, m2 – n2 and 2 mn are the sides of the triangle, then prove that the triangle is right-angled. (Use the converse of the Pythagoras theorem). Find out two Pythagorian triplets using convenient values of m and n.
Chapter: [0.02] Pythagoras Theorem
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2024 - 2025
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
