Question

12 मी रुंदीच्या रस्त्याच्या दुतर्फा समोरासमोर दोन इमारती आहेत. त्यांपैकी एकीची उंची 10 मी असून तिच्या छतावरून दुसरीच्या छताकडे पाहिले असता उन्नत कोन 60° मापाचा होतो, तर दुसऱ्या इमारतीची उंची किती?

Answer 1

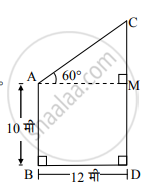
समजा, AB व CD दोन इमारतींची उंची दर्शवतात व BD ही रस्त्याची रुंदी आहे.

रेख AM ⊥ रेख CD काढा.

उन्नत कोन = ∠CAM = 60°

AB = 10 मीटर

BD = 12 मीटर

`square"ABDM"` मध्ये,

∠B = ∠D = 90°

∠M = 90°  .....[रेख AM ⊥ रेख CD]

∴ ∠A = 90°  .....[`square"ABDM"` चा उर्वरित कोन]

∴ `square"ABDM"` हा आयत आहे. ... [प्रत्येक कोनाचे माप 90°]

∴ `{:("AM" = "BD" = 12 मीटर), ("DM" = "AB" = 10 मीटर):}}` ......[आयताच्या समोरासमोरील बाजू]

ΔAMC या काटकोन त्रिकोणामध्ये,

tan 60° = `"CM"/"AM"`  ......[व्याख्येप्रमाणे]

∴ `sqrt3 = "CM"/12`

∴ CM = `12sqrt3` मीटर

आता, CD = DM + CM ........…[C - M - D]

∴ CD = `(10 + 12sqrt3)` मीटर

= 10 + 12 × 1.73

= 10 + 20.76 = 30.76

∴ दुसऱ्या इमारतीची उंची `(10 + 12sqrt3)` मीटर म्हणजेच 30.76 मीटर आहे.