Advertisements
Advertisements
Question
दीपगृहावरून एका जहाजाकडे पाहताना निरीक्षकाला 30° मापाचा अवनत कोन करावा लागतो. जर दीपगृहाची उंची 100 मी असेल तर ते जहाज दीपगृहापासून किती अंतरावर आहे?
Solution
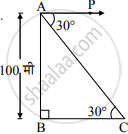
समजा, AB ही दीपगृहाची उंची आहे आणि बिंदू C हा जहाजाची जागा दर्शवतो.
अवनत कोन = ∠PAC = 30°
AB = 100 मीटर
आता, किरण AP || रेख BC
∴ ∠ACB = ∠PAC ......[व्युत्क्रम कोन]
∴ ∠ACB = 30°
AB = 100 मीटर
ΔABC या काटकोन त्रिकोणामध्ये,
tan30° = `"AB"/"BC"` .....[व्याख्येप्रमाणे]
∴ `1/sqrt3 = 100/"BC"`
∴ BC = `100sqrt3` मीटर
∴ दीपगृहापासून जहाजाचे अंतर `100sqrt3` मीटर आहे.
APPEARS IN
RELATED QUESTIONS
12 मी रुंदीच्या रस्त्याच्या दुतर्फा समोरासमोर दोन इमारती आहेत. त्यांपैकी एकीची उंची 10 मी असून तिच्या छतावरून दुसरीच्या छताकडे पाहिले असता उन्नत कोन 60° मापाचा होतो, तर दुसऱ्या इमारतीची उंची किती?
जेव्हा आपण क्षितीजसमांतर रेषेच्या वरच्या दिशेने पाहतो, तेव्हा ______ कोन होतो.
अग्निशामकदलाच्या वाहनावर बसवलेली शिडी जास्तीत जास्त 70° मापाच्या कोनातून उचलता येते. त्यावेळी तिची अधिकात अधिक लांबी 20 मी असते. शिडीचे वाहनावरील टोक जमिनीपासून 2 मी उंचीवर आहे. तर शिडीचे दुसरे टोक जमिनीपासून जास्तीत जास्त किती उंचीवर पोहोचवता येईल ? (sin 70° ≈ 0.94)
खालील प्रश्नासाठी उत्तराचा योग्य पर्याय निवडा.
जर ∠A = 30° तर tan 2A = ?
tan θ × A = sin θ, तर A = ?
`1/("cosec" theta - cot theta)` = cosec θ + cot θ हे सिद्ध करा.
∆ABC मध्ये, cos C = `12/13` असून BC = 24, तर AC = ?
जर sin A = `3/5` तर 4 tan A + 3 sin A = 6 cos A दाखवा.
एक व्यक्ती एका मंदिरापासून 50 मी. अंतरावर उभा आहे. त्या व्यक्तीने मंदिराच्या कळसाकडे पाहिले असता 45° मापाचा उन्नत कोन तयार होतो. तर त्या मंदिराची उंची किती?
बाह्यस्पर्शी असलेल्या दोन वर्तुळाच्या त्रिज्या अनुक्रमे 5 सेमी व 3 सेमी असतील तर त्यांच्या केंद्रातील अंतर किती असेल?
