Question

5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।

Answer 1

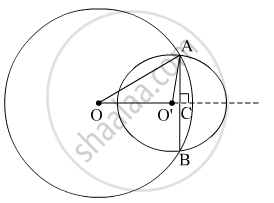
माना O और O' पर केन्द्रित वृत्त की त्रिज्या क्रमशः 5 cm और 3 cm है।

OA = OB = 5 cm

O'A = O'B = 3 cm

OO' जीवा AB का लम्ब समद्विभाजक होगा।

∴ AC = CB

यह दिया गया है कि, OO' = 4 cm

माना OC x है। इसलिए, O'C, x − 4 होगा।

ΔOAC में,

OA² = AC² + OC²

⇒ 5² = AC² + x²

⇒ 25 − x² = AC²        ... (1)

ΔO'AC में,

O'A² = AC² + O'C²

⇒ 3² = AC² + (x − 4)²

⇒ 9 = AC² + x² + 16 − 8x

⇒ AC² = − x² − 7 + 8x     ... (2)

समीकरण (1) और (2) से, हम प्राप्त करते हैं

25 − x² = − x² − 7 + 8x

8x = 32

x = 4

इसलिए, उभयनिष्ठ जीवा छोटे वृत्त के केंद्र से होकर जाता है, अर्थात, O' और इसलिए, यह छोटे वृत्त का व्यास होगा।

उभयनिष्ठ जीवा की लंबाई AB = 2 O'A = (2 × 3) cm = 6 cm.