Question

एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?

Answer 1

RS और SM पर क्रमशः लम्ब OA और OB खींचिए।

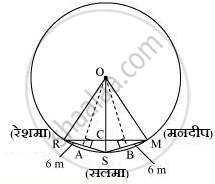
AR = AS = `6/2` = 3m

OR = OS = OM = 5m      (वृत्त की त्रिज्या)

ΔOAR में,

OA² + AR² = OR²

OA² + (3m)² = (5m)²

OA² = (25 − 9) m² = 16m²

OA = 4m

ORSM एक पतंग होगी (OR = OM और RS = SM)। हम जानते हैं कि एक पतंग के विकर्ण लंबवत होते हैं और दोनों समद्विबाहु त्रिभुजों के उभयनिष्ठ विकर्ण दूसरे विकर्ण से समद्विभाजित होते हैं।

∴ ∠RCS 90° का होगा और RC = CM

ΔORS का क्षेत्रफल = `1/2 xx OA xx RS`

`1/2 xx RC xx OS` = `1/2 xx 4 xx 6`

Rc × 5 = 24

RC = 4.8

RM = 2RC

= 2(4.8)

= 9.6

इसलिए, रेशमा और मनदीप के बीच की दूरी 9.6 m है।