Advertisements
Advertisements
Question
20m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
Solution
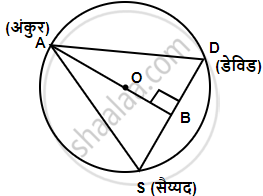
यह दिया गया है कि AS = SD = DA
अत:, ΔASD एक समबाहु त्रिभुज है।
OA (त्रिज्या) = 20m
समबाहु त्रिभुज की माध्यिकाएँ समबाहु त्रिभुज ASD के परिधि केंद्र (O) से होकर गुजरती हैं। हम यह भी जानते हैं कि माध्यिकाएं एक दूसरे को 2 : 1 के अनुपात में काटती हैं। चूंकि AB समबाहु त्रिभुज ASD की माध्यिका है, इसलिए हम लिख सकते हैं
`⇒(OA)/(OB)` = `2/1`
`⇒(20m)/(OB)` = `2/1`
`⇒OB =(20/2)m` = 10m
∴ AB = OA + OB = (20 + 10) m = 30m
ΔABD में,
AD2 = AB2 + BD2
AD2 = `(30)^2 + ((AD)/2)^2`
AD2 = `900 + 1/4AD^2`
`3/4AD^2` = 900
AD2 = 1200
AD = `20sqrt3`
इसलिए, प्रत्येक फोन की डोरी की लम्बाई `20sqrt3` m होगी।
APPEARS IN
RELATED QUESTIONS
5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केंद्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
यदि एक रेखा दो संकेंद्री वृतों (एक ही केंद्र वाले वृत्त) को, जिनका केंद्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है (देखिए आकृति में)।

एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?
एक उभयनिष्ठ कर्ण AB पर दो समकोण त्रिभुज ACB और ADB इस प्रकार खींचे गए हैं कि वे विपरीत ओर स्थित हैं। सिद्ध कीजिए कि ∠BAC = ∠BDC हैं।
एक त्रिभुज ABC का परिकेंद्र O है। सिद्ध कीजिए कि ∠OBC + ∠BAC = 90º है।
यदि एक वृत्त की दो बराबर जीवाएँ परस्पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के दो भाग दूसरी जीवा के दोनों भागों के पृथक-पृथक बराबर होते हैं।
