Advertisements
Advertisements
Question
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, तीनों भाषाओं में से कम से कम एक भाषा पढ़ते हैं।
Solution
तीन भाषाओं में से कम से कम एक की पढ़ाई करने वाले छात्रों की संख्या का गणना करें।
आकृति को देखें।
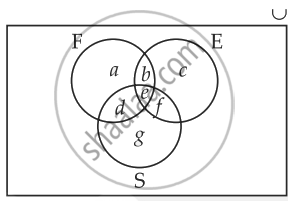
आकृति के वर्णन से
उपरोक्त समीकरणों से हमारे पास उन छात्रों की संख्या है जो कम से कम तीन भाषाओं में से एक की पढ़ाई करते हैं
APPEARS IN
RELATED QUESTIONS
यदि X और Y दो ऐसे समुच्चय हैं कि X ∪ Yमें 18, X में 8 और Y में 15 अवयव हों तो X ∩ Y में कितने अवयव होंगे?
400 व्यक्तियों के समूह में, 250 हिन्दी तथा 200 अंग्रेजी बोल सकते हैं। कितने व्यक्ति हिन्दी तथा अंग्रेजी दोनों बोल सकते हैं?
यदि S और T दो ऐसे समुच्चय हैं कि 5 में 21, T में 32 और S ∩ T में 11 अवयव हों तो S ∪ T में कितने अवयव होंगे?
यदि X और Y दो ऐसे समुच्चय हैं कि x में 40, X ∩ Y में 60 और X ∪ Y में 10 अवयव हों, तो Y में कितने अवयव होंगें?
70 व्यक्तियों के समूह में 37 कॉफी, 52 चाय पसंद करते हैं और प्रत्येक व्यक्ति दोनों मे से कम से कम एक पेय पसंद करता है, तो कितने व्यक्ति कॉफी और चाय दोनों पसंद करते हैं?
60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार पत्र H, 26 लोग समाचार पत्र T, 26 लोग समाचार पत्र I, 9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों, 8 लोग T तथा । दोनों और 3 लोग तीनों ही समाचार पत्र पढ़ते हैं, तो निम्नलिखित ज्ञात कीजिए:
- कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
- ठीक ठीक केवल एक समाचार पत्र पढ़ने वालों की संख्या।
गणित, भौतिक विज्ञान तथा रसायन विज्ञान में परीक्षा देने वाले 50 विद्यार्थियों में से प्रत्येक कम से कम एक विषय में उत्तीर्ण होता है। 37 गणित में, 24 भौतिक विज्ञान में तथा 43 रसायन विज्ञान में उत्तीर्ण होते हैं। यदि गणित और भौतिक विज्ञान में अधिकतम 19, गणित और रसायन विज्ञान में अधिकतम 29 तथा भौतिक विज्ञान और रसायन विज्ञान में अधिकतम 20 उत्तीर्ण होते हैं, तो तीनों विषयों में उत्तीर्ण होने वाले विद्यार्थियों की अधिकतम संभव संख्या कितनी है?
60 विद्यार्थियों की एक कक्षा में, 25 विद्यार्थी क्रिकेट और 20 विद्यार्थी टेनिस खेलते हैं तथा 10 विद्यार्थी दोनों ही खेल खेलते हैं। उन विद्यार्थियों की संख्या ज्ञात कीजिए जो इन दोनों में से कोई भी खेल नहीं खेलते हैं।
किसी विद्यालय के 200 विद्यार्थियों के सर्वेक्षण (Survey) से ज्ञात हुआ कि 120 विद्यार्थी गणित, 90 भौतिक विज्ञान तथा 70 रसायन विज्ञान पढ़ते हैं। 40 गणित और भौतिक विज्ञान, 30 भौतिक विज्ञान और रसायन विज्ञान, 50 रसायन विज्ञान और गणित पढ़ते हैं तथा 20 इन विषयों में से कोई भी विषय नहीं पढ़ते हैं। उन विद्यार्थियों की संख्या ज्ञात कीजिए, जो इन तीनों ही विषयों को पढ़ते हैं।
किसी शहर के 10,000 परिवारों के बारे में ज्ञात होता है कि 40% समाचार पत्र A, 20% समाचार पत्र B, 10% समाचार पत्र C, 5% समाचार पत्र A और B, 3% समाचार पत्र B और C तथा 4% समाचार पत्र A और C खरीदते हैं। यदि 2% परिवार तीनों ही समाचार पत्र खरीदते हैं, तो उन परिवारों की संख्या ज्ञात कीजिए जो केवल समाचार पत्र A खरीदते हैं।
किसी शहर के 10,000 परिवारों के बारे में ज्ञात होता है कि 40% समाचार पत्र A, 20% समाचार पत्र B, 10% समाचार पत्र C, 5% समाचार पत्र A और B, 3% समाचार पत्र B और C तथा 4% समाचार पत्र A और C खरीदते हैं। यदि 2% परिवार तीनों ही समाचार पत्र खरीदते हैं, तो उन परिवारों की संख्या ज्ञात कीजिए जो A, B तथा C में से कोई भी समाचार पत्र नहीं खरीदते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, केवल फ्रांसीसी पढ़ते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, केवल संस्कृत पढ़ते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, अंग्रेजी और संस्कृत पढ़ते हैं परंतु, फ्रांसीसी नहीं पढ़ते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, फ्रांसीसी और संस्कृत पढ़ते हैं परंतु अंग्रेजी नहीं पढ़ते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, फ्रांसीसी और अंग्रेजी पढ़ते हैं परंतु संस्कृत नहीं पढ़ते हैं।
50 विद्यार्थियों के एक समूह में फ्रांसीसी, अंग्रेजी और संस्कृत विषयों का अध्ययन करने वालों की संख्या निम्नलिखित प्रकार है: फ्रांसीसी = 17, अंग्रेजी = 13, संस्कृत = 15, फ्रांसीसी और अंग्रेजी = 09, अंग्रेजी और संस्कृत = 04, फ्रांसीसी और संस्कृत = 05, अंग्रेजी, फ्रांसीसी और संस्कृत = 03 उन विद्यार्थियों की संख्या ज्ञात कीजिए जो, तीनों भाषाओं में से एक भी भाषा नहीं पढ़ते हैं।
60 विद्यार्थियों की एक कक्षा में 25 विद्यार्थी क्रिकेट, 20 विद्यार्थी टेनिस और 10 विद्यार्थी दोनों ही खेल खेलते हैं, तो दोनों में से कोई भी खेल नहीं खेलने वाले विद्यार्थियों की संख्या ______
यदि 840 व्यक्तियों वाले किसी नगर में 450 व्यक्ति हिंदी, 300 व्यक्ति अंग्रेजी और 200 व्यक्ति दोनों ही विषय पढ़ते हैं, तो दोनों में से कोई भी विषय नहीं पढ़ने वाले व्यक्तियों की संख्या ______
यदि X = {8n − 7n − 1 ∣ n ∈ N} और Y = {49n − 49 ∣ n ∈ N}, तो ______
यदि समुच्चय A और B निम्नलिख़ित प्रकार से परिभाषित हैं, A = `{(x,y)∣y=1/x,0≠x∈R}` B = {(x; y) ∣ y = −x, x ∈ R}, तो ______
मान लीजिए कि S = {x ∣ x 100 से छोटा 3 का एक धनात्मक गुणज है},
P = {x ∣ x, 20 से छोटी एक अभाज्य संख्या है}, तो n(S) + n(P) = ______ है।
जब A = ϕ, तो P(A) में अवयवों की संख्या ______ है।
