Advertisements
Advertisements
Question
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears a two-digit number.
Solution
We have total number of discs = 90
Total number of possible outcomes = 90
Since the two-digit numbers are 10, 11, 12, ....., 90.
∴ Number of two-digit numbers: 90 − 9 = 81
∴ Number of favourable outcomes = 81
∴ P (getting a two-digit number) = `"Number of favourable outcomes"/"Total number of possible outcomes"`
= `81/90`
= `9/10`
RELATED QUESTIONS
The sum of the probabilities of all the elementary events of an experiment is _________.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out an orange flavoured candy?
A die is numbered in such a way that its faces show the number 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:
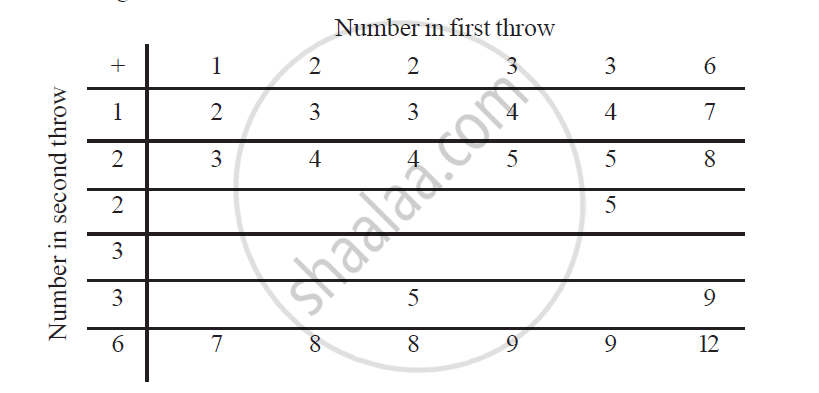
What is the probability that the total score is
(i) even? (ii) 6? (iii) at least 6?
A die is thrown. Find the probability of getting:
an even prime number
In a simultaneous throw of a pair of dice, find the probability of getting a number other than 5 on any dice.
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is a ten
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a king of red colour.
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is jack
A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability? of obtaining a total of 6?
Five cards—ten, jack, queen, king, and an ace of diamonds are shuffled face downwards.One card is picked at random If a king is drawn first and put aside, what is the probability that the second card picked up is the ace?
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is not red?
Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket?
From a well-shuffled deck of 52 playing-cards, one card is drawn. Find the probability that the card drawn will be a black card.
From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is a black card.
A bag contains 100 identical marble stones which are numbered 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears a perfect square number.
Tickets numbered 2, 3, 4, 5, ..., 100, 101 are placed in a box and mixed thoroughly. One ticket is drawn at random from the box. Find the probability that the number on the ticket is a number which is a perfect square.
If the probability of occurence of an event is p then the probability of non-happening of this event is (p − 1).
Namita tossed a coin once. What is the probability of getting Head?
A coin is tossed two times. Find the probability of getting at most one head.
Cards with numbers 2 to 101 are placed in a box. A card is selected at random. Find the probability that the card has a square number
