Advertisements
Advertisements
Question
A fair die is rolled. If face 1 turns up, a ball is drawn from Bag A. If face 2 or 3 turns up, a ball is drawn from Bag B. If face 4 or 5 or 6 turns up, a ball is drawn from Bag C. Bag A contains 3 red and 2 white balls, Bag B contains 3 red and 4 white balls and Bag C contains 4 red and 5 white balls. The die is rolled, a Bag is picked up and a ball is drawn. If the drawn ball is red; what is the probability that it is drawn from Bag B?
Solution
Let E1, E2, E3 be the events that a die is thrown and getting 1, 2 or 3 and 4 or 5 or 6 respectively.
`"P"("E"_1) = 1/6 , "P"("E"_2) = 2/6 , "P"("E"_3) = 3/6`
Let A be the event that drawn ball is red
`"P"("A"//"E"_1) = 3/5 , "P"("A"//"E"_2) = 3/7 , "P"("A"//"E"_3) = 4/9`
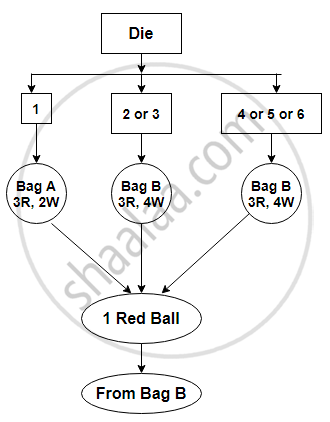
Required probability i.e. drawn ball is red from bag B is :
`"P"("E"_2//"A") = ("P"("E"_2) xx "P"("A"//"E"_2))/("P"("E"_1) xx "P"("A"//"E"_1) + "P"("E"_2) xx "P"("A"//"E"_2) + "P"("E"_3)xx "P"("A"//"E"_3))`
`= (2/6 xx 3/7)/(1/6 xx 3/5 + 2/6 xx 3/7 + 3/6 xx 4/9)`
`= (1/7)/(1/10 + 1/7 + 2/9)`
`= 1/7 xx (7 xx 9 xx 10)/293 = 90/293`
APPEARS IN
RELATED QUESTIONS
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all balls in the bag are white?
Let E and F be events with `P(E) = 3/5, P(F) = 3/10 and P(E ∩ F) = 1/5`. Are E and F independent?
If A and B are two events such that `P(A) = 1/4, P(B) = 1/2 and P(A ∩ B) = 1/8`, find P (not A and not B).
Probability of solving specific problem independently by A and B are `1/2` and `1/3` respectively. If both try to solve the problem independently, find the probability that
- the problem is solved
- exactly one of them solves the problem.
One card is drawn at random from a well-shuffled deck of 52 cards. In which of the following case is the events E and F independent?
E : ‘the card drawn is a king or queen’
F : ‘the card drawn is a queen or jack’
Two events, A and B, will be independent if ______.
The odds against a certain event are 5: 2 and odds in favour of another independent event are 6: 5. Find the chance that at least one of the events will happen.
The odds against student X solving a business statistics problem are 8: 6 and odds in favour of student Y solving the same problem are 14: 16 What is the probability that neither solves the problem?
Two hundred patients who had either Eye surgery or Throat surgery were asked whether they were satisfied or unsatisfied regarding the result of their surgery
The follwoing table summarizes their response:
| Surgery | Satisfied | Unsatisfied | Total |
| Throat | 70 | 25 | 95 |
| Eye | 90 | 15 | 105 |
| Total | 160 | 40 | 200 |
If one person from the 200 patients is selected at random, determine the probability that person was unsatisfied given that the person had eye surgery
Two dice are thrown together. Let A be the event 'getting 6 on the first die' and B be the event 'getting 2 on the second die'. Are the events A and B independent?
Solve the following:
If P(A) = `"P"("A"/"B") = 1/5, "P"("B"/"A") = 1/3` the find `"P"("A'"/"B")`
Solve the following:
Find the probability that a year selected will have 53 Wednesdays
Solve the following:
Consider independent trails consisting of rolling a pair of fair dice, over and over What is the probability that a sum of 5 appears before sum of 7?
Solve the following:
A machine produces parts that are either good (90%), slightly defective (2%), or obviously defective (8%). Produced parts get passed through an automatic inspection machine, which is able to detect any part that is obviously defective and discard it. What is the quality of the parts that make it throught the inspection machine and get shipped?
10% of the bulbs produced in a factory are of red colour and 2% are red and defective. If one bulb is picked up at random, determine the probability of its being defective if it is red.
If A and B are independent events such that 0 < P(A) < 1 and 0 < P(B) < 1, then which of the following is not correct?
If A and B′ are independent events then P(A′ ∪ B) = 1 – ______.
Refer to Question 1 above. If the die were fair, determine whether or not the events A and B are independent.
The probability that at least one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate `"P"(bar"A") + "P"(bar"B")`
Two dice are thrown together and the total score is noted. The events E, F and G are ‘a total of 4’, ‘a total of 9 or more’, and ‘a total divisible by 5’, respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.
A and B are events such that P(A) = 0.4, P(B) = 0.3 and P(A ∪ B) = 0.5. Then P(B′ ∩ A) equals ______.
If two events are independent, then ______.
If the events A and B are independent, then P(A ∩ B) is equal to ______.
Let E1 and E2 be two independent events. Let P(E) denotes the probability of the occurrence of the event E. Further, let E'1 and E'2 denote the complements of E1 and E2, respectively. If P(E'1 ∩ E2) = `2/15` and P(E1 ∩ E'2) = `1/6`, then P(E1) is
Let Bi(i = 1, 2, 3) be three independent events in a sample space. The probability that only B1 occur is α, only B2 occurs is β and only B3 occurs is γ. Let p be the probability that none of the events Bi occurs and these 4 probabilities satisfy the equations (α – 2β)p = αβ and (β – 3γ) = 2βy (All the probabilities are assumed to lie in the interval (0, 1)). Then `("P"("B"_1))/("P"("B"_3))` is equal to ______.
The probability of the event A occurring is `1/3` and of the event B occurring is `1/2`. If A and B are independent events, then find the probability of neither A nor B occurring.
