Advertisements
Advertisements
Question
A needle of a sewing machine moves along a path of amplitude 4 cm with a frequency of 5 Hz. Find its acceleration `(1/30)` s after it has crossed the mean position.
Solution
Data: A = 4 cm, n = 5 Hz, t = `(1/30)` s, a = - ω2 x, |a| = ω2x
as x = A sin ω t
∴ |a| = ω2 A sin ω t
`= (2 π " n")^2 "A" sin (2 π " n") xx 1/30`
`= 4 pi^2 "n"^2 " A" sin (2 pi 5) 1/30`
`= 4pi^2 xx 25 xx 4 sin (10 pi)/30`
`= 100 pi^2 xx 4 sin pi/3`
`= 100pi^2 xx cancel(4)^2 xx sqrt3/cancel(2)_1`
`= 100 pi^2 xx 2 xx 1.732`
`= 100 xx pi^2 xx 3.464`
`= 346.4 xx 9.87`
= 3420 cm/s2
= 3420 × 10-2 m/s2
|a| = 34.2 m/s2
APPEARS IN
RELATED QUESTIONS
Potential energy of a particle performing linear S.H.M. is 0.1 π2x2 joule. If the mass of the particle is 20 g, find the frequency of S.H.M.
Two S.H.M.’s have zero phase difference and equal amplitudes A. The resultant amplitude on their composition will be ______
What is the amplitude of S.H.M.
A particle performing S.H.M. has velocities of 8 cm/s and 6 cm/s at displacements of 3 cm and 4 cm respectively. Calculate the amplitude and period of S.H.M.
Obtain an expression for the resultant amplitude of, the composition of two S.H.M.’s having the same period along the same path.
Two wires of different materials have same length L and same diameter d. The second wire is connected at the end of the first wire and forms one single wire of double the length. This wire is subjected to stretching force F to produce the elongation l. The two wires have ______.
In amplitude modulation,
The total energy of the body executing S.H.M. is E. The kinetic energy of the body, when the displacement is half of the amplitude is ______.
When a mass is hung from a light spring, the spring extends by 10 cm. If the mass is pulled down and let go, it executes S.H.M. with a time period (g = 10 m/s2) ____________.
A particle is executing S.H.M. with amplitude of 4 cm and time period 12 s. The time taken by the particle in going from its mean position to a position of displacement equal to 2 cm is T1 The time taken from this displaced position of 2 cm to reach the extreme position is T2. T1/ T2 will be____________.
If 'x', 'v' and 'a' denote the displacement, velocity and acceleration of a particle respectively executing SHM of periodic time t, then which one of the following does not change with time?
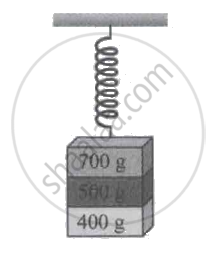
Three masses 700 g, 500 g, and 400 g are suspended at the end of a spring and are in equilibrium as shown in figure. When the 700 g mass is removed, the system oscillates with a period of 3 seconds; when the 500 g mass is also removed, it will oscillate with a period of ____________.
The equation of S.H.M. of a particle of amplitude 4 cm performing 150 oscillations per minute starting with an initial phase 30° is ____________.
The amplitude of sound is doubled and the frequency is reduced to one fourth. The intensity of sound at the same point will be ____________.
A body of mass 1 kg is suspended from a spring of negligible mass. Another body of mass 500 g moving vertically upwards hits the suspended body with a velocity 3 ms-1 and gets embedded in it. If the frequency of oscillation of the system of the two bodies after collision `10/pi` Hz, the amplitude of motion and the spring constant are respectively ____________.
Two trains are moving towards each other with speeds of 20m/s and 15 m/s relative to the ground. The first train sounds a whistle of frequency 600 Hz. The frequency of the whistle heard by a passenger in the second train before the train meets, is ______. (the speed of sound in air is 340 m/s)
A mass is suspended from a vertical spring which is executing S.H.M. of frequency 5 Hz. The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is ______. [acceleration due to gravity g = 10 m/s2]
A particle performing SHM starts equilibrium position and its time period is 16 seconds. After 2 seconds its velocity is π m/s. Amplitude of oscillation is ______. `(cos 45° = 1/sqrt2)`
A mass m1 connected to a horizontal spring performs SHM with amplitude A. While mass m1 is passing through mean position, another mass m2 is placed on it so that both the masses move together with amplitude A1. The ratio of `"A"_1/"A"` is ______. (m2 < m1)
The motion of a particle varies with time according to the relation y = a sin ω t + a cos ω t. Then, ______.
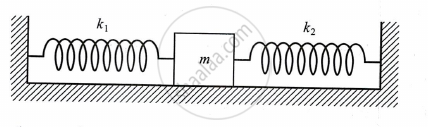
A block of mass m, connected to two springs of spring constants k1 and k2 as shown, oscillates on a smooth horizontal surface. What is the effective spring constant of the oscillation?
Light of a certain colour has 2500 waves to the millimetre in air. What is its frequency?
