Advertisements
Advertisements
Question
A parallel-plate capacitor having plate area 400 cm2 and separation between the plates 1⋅0 mm is connected to a power supply of 100 V. A dielectric slab of thickness 0⋅5 mm and dielectric constant 5⋅0 is inserted into the gap. (a) Find the increase in electrostatic energy. (b) If the power supply is now disconnected and the dielectric slab is taken out, find the further increase in energy. (c) Why does the energy increase in inserting the slab as well as in taking it out?
Solution
The capacitance of the capacitor without the dielectric slab is given by
`C_1 = (∈_0A)/d`
⇒ `C = ((8.85 xx 10^-12) xx (400 xx 10^-4))/((1.0 xx 10^-3))`
⇒ `C = 3.54 xx 10^-10 "F"`
When the dielectric slab is inserted, the capacitance becomes
`C^' = (∈_0A)/((d-t+t/k))`
⇒ `C^' = ((8.85 xx 10^-12) xx (400 xx 10^-4))/((1 xx 10^-3 - 0.5 xx 10^-3+(0.5 xx 10^-3)/5)`
⇒ `C^' =(5 xx (8.85 xx 10^-12) xx (400 xx 10^-4))/((6 xx 0.5 xx 10^-3))`
⇒ `C^' = 5.9 xx 10^-10 "F"`
(a) Increased electrostatic energy :
`ΔE = 1/2C^'V^2 - 1/2 CV^2`
⇒`ΔE = 1/2(5.9 - 3.54) xx 10^-10 xx (100)^2`
⇒ `ΔE = 1.18 xx 10^-6 "J" = 1.18 "uJ"`
(b)
Charge on the capacitor containing dielectric is,
`Q^' = C^'V`
⇒ `Q^' = 5.9 xx 10^-10 xx 100`
⇒ `Q^' = 5.9 xx 10^-8 C`
Potential difference across the capacitor after removing battery and then dielectric is,
`V^' = Q^'/C`
⇒ `V^' = (5.9 xx 10^-8)/(3.54 xx 10^-10)`
⇒ `V^' = 166 V`
Increased electrostatic energy ,
`ΔE^' = 1/2 CV^'2 - 1/2C^'V^2`
⇒ `ΔE^' = 1/2[3.54 xx 10^-10 xx (166)^2 - 5.9 xx 10^-10 xx (100)^2]`
⇒ `ΔE^' = 1.92 xx 10^-6 J = 1.92 "uJ"`
(c) When the battery is connected, energy is increased after insertion of the dielectric slab because of the increase in the capacitance of the capacitor. Now, capacitor will abstract more change from the battery.
When the battery is disconnected, and dielectric slab is taken out then energy stored in the will increase because of increase of potential difference across the capacitor.
APPEARS IN
RELATED QUESTIONS
Electric intensity due to a charged sphere at a point outside the sphere decreases with...................
Write a relation for polarisation `vecP`of a dielectric material in the presence of an external electric field `vecE .`
How does polarised dielectric modify the original external field?
Define the terms polarization of a dielectric and write its relation with susceptibility.
Two metal plates having charges Q, −Q face each other at some separation and are dipped into an oil tank. If the oil is pumped out, the electric field between the plates will
A dielectric slab is inserted between the plates of an isolated charged capacitor. Which of the following quantities will remain the same?
Explain briefly, using a proper diagram, the difference in behaviour of a conductor and a dielectric in the presence of external electric field.
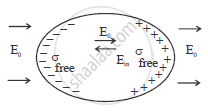
Define the term polarization of a dielectric and write the expression for a linear isotropic dielectric in terms of electric field.
Two metal spheres, one of radius R and the other of radius 2R, both have same surface charge density σ. They are brought in contact and separated. What will be new surface charge densities on them?
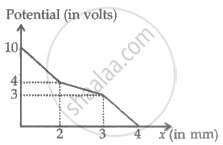
A capacitor filled partially with dielectric material of dielectric constant 'k'. Its electric potential versus position graph is as shown. The distance between the two plates is 4 mm. The dielectric constant of the medium is ______.
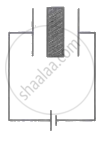
An isolated parallel plate capacitor is maintained at a certain potential difference. When a 3 mm thick slab is introduced between the plates, in order to maintain the same potential difference the distance between the plates is increased by 2.4 mm. The dielectric constant of the slab will be ______.
