Advertisements
Advertisements
Question
A particle of mass m is attatched to three springs A, B and C of equal force constants kas shown in figure . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.
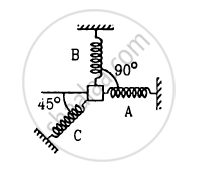
Solution
(a) Let us push the particle lightly against the spring C through displacement x.
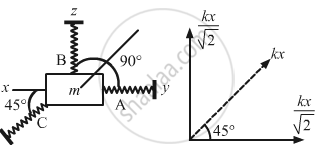
As a result of this movement, the resultant force on the particle is kx.
The force on the particle due to springs A and B is \[\frac{kx}{\sqrt{2}}\] .
Total Resultant force \[= kx + \sqrt{\left( \frac{kx}{\sqrt{2}} \right)^2 + \left( \frac{kx}{\sqrt{2}} \right)^2}\]
= kx + kx = 2kx
Acceleration is given by \[= \frac{2kx}{m}\]
\[\text { Time period }= 2\pi\sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\]
\[ = 2\pi\sqrt{\frac{x}{2kx/m}}\]
\[ = 2\pi\sqrt{\frac{m}{2k}}\]
APPEARS IN
RELATED QUESTIONS
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
Which of the following example represent periodic motion?
An arrow released from a bow.
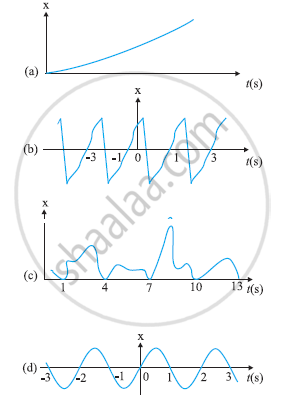
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
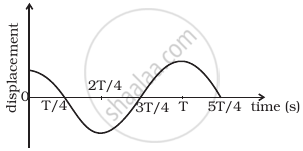
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
What are the two basic characteristics of a simple harmonic motion?
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
