Advertisements
Advertisements
Question
A short magnet is moved along the axis of a conducting loop. Show that the loop repels the magnet if the magnet is approaching the loop and attracts the magnet if it is going away from the loop.
Solution
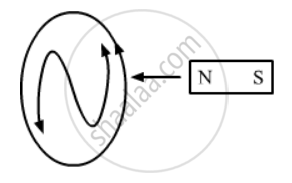
Consider the above situation in which a magnet is moved towards a conducting circular loop. The north pole of the magnet faces the loop. As the magnet comes closer to the loop, the magnetic field increases; hence, flux through the loop increases. According to Lenz's law, the direction of induced current is such that it opposes the magnetic field that has induced it. Thus, the induced current produces a magnetic field in the direction opposite to the original field; hence, the loop repels the magnet.
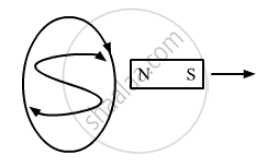
On the other hand, when the magnet is going away from the loop, the magnetic field decreases. Hence, flux through the loop decreases. According to Lenz's law, the induced current produces a magnetic field in the opposite direction of the original field; hence, the loop attracts the magnet.
APPEARS IN
RELATED QUESTIONS
State Lenz's law. Illustrate, by giving an example, how this law helps in predicting the direction of the current in a loop in the presence of a changing magnetic flux.
Use Lenz’s law to determine the direction of induced current in the situation described by the figure:
A wire of irregular shape turning into a circular shape.
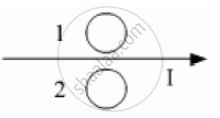
Predict the directions of induced currents in metal rings 1 and 2 lying in the same plane where current I in the wire is increasing steadily.
A bar magnet is released from rest along the axis of a very long, vertical copper tube. After some time the magnet ____________ .
Two circular loops of equal radii are placed coaxially at some separation. The first is cut and a battery is inserted in between to drive a current in it. The current changes slightly because of the variation in resistance with temperature. During this period, the two loops _______________ .
A bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
(a) The south pole faces the ring and the magnet moves towards it.
(b) The north pole faces the ring and the magnet moves towards it.
(c) The south pole faces the ring and the magnet moves away from it.
(d) The north pole faces the ring and the magnet moves away from it.
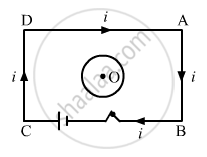
Consider the situation shown in figure. If the closed loop is completely enclosed in the circuit containing the switch, the closed loop will show _______________ .
Explain, with the help of a suitable example, how we can show that Lenz's law is a consequence of the principle of conservation of energy.
Which of the following statements is not correct?
2 A 40 kg boy whose legs are 4 cm in area and 50 cm long falls through a height of 2 m without breaking his leg bones. If the bones can withstand stress of 0.9 x 108 N/m2. The Young's modulus for the material of the bone is ______.
Young's modulus for aluminium is 7 × 1010 Pa. The force needed to stretch an aluminium wire of diameter 2 mm and length 800 mm by 1 mm is ______.
For a coil having L = 2 mH, current flows at the rate of 10-3 AIS. The e.m.f induced is
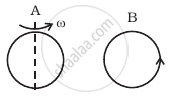
There are two coils A and B as shown in figure. A current starts flowing in B as shown, when A is moved towards B and stops when A stops moving. The current in A is counterclockwise. B is kept stationary when A moves. We can infer that ______.

Same as problem 4 except the coil A is made to rotate about a vertical axis (figure). No current flows in B if A is at rest. The current in coil A, when the current in B (at t = 0) is counterclockwise and the coil A is as shown at this instant, t = 0, is ______.
A metallic ring of mass m and radius `l` (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is Bz = Bo (1 + λz). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m, B, λ and acceleration due to gravity g.
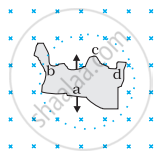
Predict the direction of induced current in the situation described by the following figure.