Advertisements
Advertisements
Question
A transverse wave is produced on a stretched string 0.9 m long and fixed at its ends. Find the speed of the transverse wave, when the string vibrates while emitting the second overtone of frequency 324 Hz.
Solution
For second overtone frequency (or third harmonic mode of vibration) n = 3.
APPEARS IN
RELATED QUESTIONS
When longitudinal wave is incident at the boundary of denser medium, then............................
- compression reflects as a compression.
- compression reflects as a rarefaction.
- rarefaction reflects as a compression.
- longitudinal wave reflects as transverse wave.
When a transverse wave on a string is reflected from the free end, the phase change produced is ..............
(a) zero rad
(b) ` pi/2 ` rad
(c) `(3pi)/4` rad
(d) `pi` rad
A wire of density ‘ρ’ and Young’s modulus ‘Y’ is stretched between two rigid supports separated by a distance ‘L’ under tension ‘T’. Derive an expression for its frequency in fundamental mode. Hence show that `n=1/(2L)sqrt((Yl)/(rhoL))` where symbols have their usual meanings
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = cos x sin t + cos 2x sin 2t
Explain why (or how): Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
Explain why (or how) Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases
Explain why (or how) The shape of a pulse gets distorted during propagation in a dispersive medium.
You are walking along a seashore and a mild wind is blowing. Is the motion of air a wave motion?
A transverse wave travels along the Z-axis. The particles of the medium must move
Longitudinal waves cannot
A particle on a stretched string supporting a travelling wave, takes 5⋅0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2⋅0 cm. Find the frequency, the wavelength and the wave speed.
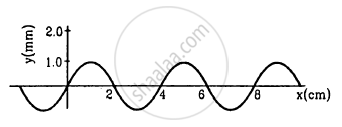
Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm s−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
Consider the following statements about sound passing through a gas.
(A) The pressure of the gas at a point oscillates in time.
(B) The position of a small layer of the gas oscillates in time.
A transverse wave described by \[y = \left( 0 \cdot 02 m \right) \sin \left( 1 \cdot 0 m^{- 1} \right) x + \left( 30 s^{- 1} \right)t\] propagates on a stretched string having a linear mass density of \[1 \cdot 2 \times {10}^{- 4} kg m^{- 1}\] the tension in the string.
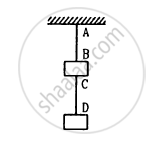
Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.
If the speed of a transverse wave on a stretched string of length 1 m is 60 m−1, what is the fundamental frequency of vibration?
A steel wire of mass 4⋅0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) What could be the maximum value of the fundamental frequency? (b) If transverse waves can travel on this string at a speed of 40 m s−1, what is its length?
A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220 m s−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0⋅5 cm, write a suitable equation describing the motion.
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
The equation of a standing wave, produced on a string fixed at both ends, is
\[y = \left( 0 \cdot 4 cm \right) \sin \left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
What could be the smallest length of the string?
The phenomenon of beats can take place
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
