Advertisements
Advertisements
Question
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
Solution
Let ABC be the equilateral triangle with side l/3 and centre M.

(a)
\[\text{In } ∆ AOB, \]
\[AO = \sqrt{\left( \frac{l}{3} \right)^2 - \left( \frac{I}{6} \right)^2}\]
\[ = l\sqrt{\frac{1}{9} - \frac{1}{36}} = l\sqrt{\frac{4 - 1}{36}} = l\sqrt{\frac{1}{12}}\]
\[ \therefore \text{ MO }= \frac{1}{3} \times l\sqrt{\frac{1}{12}} = \frac{l}{6\sqrt{3}}\]
The angles made by points B and C with centre M are \[\theta_1 = 60^\circ \text{ and } \theta_2 = 60^\circ \]
Separation of the point from the wire, d = MO = \[\frac{l}{6\sqrt{3}}\]
Thus, the magnetic field due to current in wire BC is given by
\[B = \frac{\mu_0 i}{4\pi d}(\sin \theta_1 + \sin \theta_2 )\]
\[ \Rightarrow B = \frac{\mu_0 i}{4\pi\frac{l}{6\sqrt{3}}}(\sin 60 + \sin 60)\]
\[\Rightarrow B = \frac{\mu_0 i}{4\pi l}6\sqrt{3} \times \sqrt{3}\]
Now,
Net magnetic field at M = Magnetic field due to wire BC + Magnetic field due to wire CA + Magnetic field due to wire AB
Since all wires are the same \[B_{net} = 3B\]
\[= \frac{27 \mu_0 i}{\pi l}\]
It is perpendicular to the plane in outward direction if the current is anticlockwise and perpendicular to the plane in inward direction if the current is clockwise.
(b) 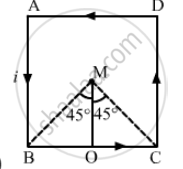
The angles made by points B and C with centre M are \[\theta_1 = 45^\circ \text{ and } \theta_2 = 45^\circ \] , respectively.
Separation of the point from the wire, d = l/8
Thus, the magnetic field due to current in wire BC is given by
\[B = \frac{\mu_0 i}{4\pi d}(\sin \theta_1 + \sin \theta_2 )\]
\[ \Rightarrow B = \frac{\mu_0 i}{4\pi\frac{l}{8}}(\sin 45 + \sin 45)\]
\[ = \frac{2\sqrt{2} \mu_0 i}{\pi l}\]
Since all wires are the same,
Net magnetic field at M = 4 × Magnetic field due to wire BC
\[\Rightarrow B_{net} = 4B =\] \[\frac{8\sqrt{2} \mu_0 i}{\pi l}\]
APPEARS IN
RELATED QUESTIONS
State Biot – Savart law.
Using Biot − Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop?
State Biot-Savart law.
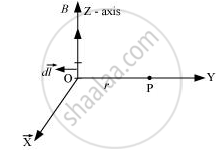
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State Biot Savart law.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
The magnetic field at any point on the axis of a current element is ______
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
