Advertisements
Advertisements
Question
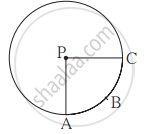
आकृतीत A(P-ABC) = 154 चौसेमी आणि वर्तुळाची त्रिज्या 14 सेमी असेल, तर
(1) ∠APC चे माप काढा.
(2) कंस ABC ची लांबी काढा.
Solution
दिलेले: A(P-ABC) = 154 सेमी2
त्रिज्या (r) = 14 सेमी
उकल:
(1) समजा, ∠APC = θ
A(P-ABC) = `θ/360 xx pir^2`
∴ 154 = `θ/360 xx 22/7 xx 14^2`
∴ θ = `(154 xx 360 xx 7)/(22 xx 14^2) = (154 xx 360 xx 7)/(22 xx 14 xx 14) = (7 xx 360)/(14 xx 2) = 360/(2 xx 2) = 90^circ`
∴ ∠APC = 90°
(2) कंस ABC ची लांबी = `θ/360 xx 2pir`
= `90/360 xx 2 xx 22/7 xx 14`
= `1/4 xx 2 xx 22 xx 2`
∴ कंस ABC ची लांबी 22 सेमी आहे.
APPEARS IN
RELATED QUESTIONS
वर्तुळाची त्रिज्या 10 सेमी आहे. वर्तुळकंसाचे माप 54° असल्यास त्या कंसाने मर्यादित केलेल्या वर्तुळपाकळीचे क्षेत्रफळ काढा. (π =3.14)
वर्तुळपाकळीची त्रिज्या 3.5 सेमी असून तिच्या वर्तुळकंसाची लांबी 2.2 सेमी आहे, तर वर्तुळपाकळीचे क्षेत्रफळ काढा.
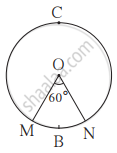
शेजारील आकृतीत वर्तुळाची त्रिज्या 7 सेमी आहे आणि m(कंस MBN) = 60° तर
(1) वर्तुळाचे क्षेत्रफळ काढा.
(2) A(O - MBN) काढा.
(3) A(O - MCN) काढा.
3.4 सेमी त्रिज्या असलेल्या वर्तुळपाकळीची परिमिती 12.8 सेमी आहे तर वर्तुळपाकळीचे क्षेत्रफळ काढा.
वर्तुळपाकळीची त्रिज्या 7 सेमी आहे. जर वर्तुळपाकळीच्या कंसाचे माप पुढीलप्रमाणे दिलेले आहे, तर त्या वर्तुळपाकळीचे क्षेत्रफळ काढा.
30°
वर्तुळपाकळीची त्रिज्या 7 सेमी आहे. जर वर्तुळपाकळीच्या कंसाचे माप पुढीलप्रमाणे दिलेले आहे, तर त्या वर्तुळपाकळीचे क्षेत्रफळ काढा.
3 काटकोन
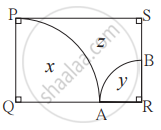
आकृतीत `square`PQRS हा आयत असून PQ = 14 सेमी, QR = 21 सेमी, तर आकृतीत दाखविलेल्या x, y आणि z या प्रत्येक भागाचे क्षेत्रफळ काढा.
जर वर्तुळाचा परीघ व वर्तुळाचे क्षेत्रफळ यांचे गुणोत्तर 2ः7 असेल तर वर्तुळाचा परीघ किती?
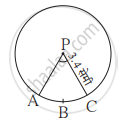
आकृतीत P हा वर्तुळाचा केंद्र असून रेख AB ही जीवा आहे. PA = 8 सेमी आणि जीवा AB वर्तुळकेंद्रापासून 4 सेमी अंतरावर असेल, तर रेखांकित भागाचे क्षेत्रफळ A काढा. (π = 3.14, `sqrt3` = 1.73)

वर्तुळपाकळी A-PCQ मध्ये `square`ABCD हा चौरस आहे. C - BXD या पाकळीची त्रिज्या 20 सेमी असेल तर रेखांकित भागाचे क्षेत्रफळ काढण्यासाठी खालील कृती करा.
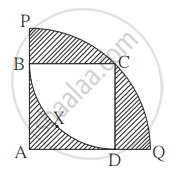
उकल: चौरस ABCD ची बाजूृ = वर्तुळपाकळी C - BXD ची त्रिज्या = `square` सेमी
चौरसाचे क्षेत्रफळ = बाजूृ2 = `square^2` = `square` ...(l)
चौरसातील रेखांकित भागाचे क्षेत्रफळ = चौरस ABCD चे क्षेत्रफळ - वर्तुळपाकळी C - BXD चे क्षेत्रफळ
= `square - θ/360 xx pir^2`
= `square - 90/360 xx 3.14/1 xx 400/1`
= `square - 314`
= `square`
मोठ्या वर्तुळपाकळीची त्रिज्या = चौरस ABCD च्या कर्णाची लांबी
= `20sqrt2`
माेठ्या वर्तुळपाकळीतील चौरसाबाहेरील रेखांकित भागाचे क्षेत्रफळ
= वर्तुळपाकळी A - PCQ चे क्षेत्रफळ - चौरस ABCD चे क्षेत्रफळ
= A(A - PCQ) - A(`square` ABCD)
= `(θ/360 xx pi xx r^2) - square^2`
= `90/360 xx 3.14(20sqrt2)^2 - (20)^2`
= `square - square`
= `square`
∴ रेखांकित भागाचे एकूण क्षेत्रफळ = 86 + 228 = 314 चौसेमी
