Advertisements
Advertisements
Question
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है की पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 मीटर है। पेड़ की उँचाई ज्ञात कीजिए।
Solution
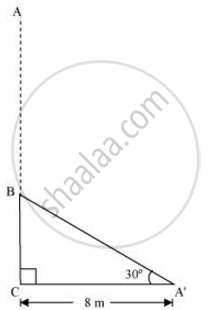
बता दें कि AC असली पेड़ था। आंधी के कारण यह दो भागों में टूट गया। टूटा हुआ हिस्सा A'B जमीन से 30° बना रहा है।
ΔABC में,
`("BC")/("AC")` = tan 30°
`("BC")/8 = 1/sqrt3`
`"BC" = (8/sqrt3)m`
`("AC")/("AB")` = cos 30°
`8/("AB") = sqrt3/2`
`"AB" = ((16)/sqrt3)m`
पेड़ की उँचाई = AB + BC
= `(16/sqrt3+8/sqrt3)m`
= `24/sqrt3` m
= `8sqrt3` m
इसलिए पेड़ की उँचाई `8sqrt3` m है।
APPEARS IN
RELATED QUESTIONS
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बिच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो की मीनार के पाद की ओर एक समान चाल से जाता है। छ: सेकेंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
6 m ऊँचे एक खंभे की छाया भूमि पर `2sqrt3` m लंबी है। तब, उस समय सूर्य का उन्नयन कोण ______ है।
यदि एक मीनार की छाया की लंबाई बढ़ रही है, तो सूर्य का उन्नयन कोण भी बढ़ रहा है।
सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
15 मीटर लंबी एक सीढ़ी एक ऊर्ध्वाधर दीवार के ठीक ऊपरी सिरे पर पहुँच पाती है। यदि सीढ़ी इस समय दीवार से 60° का कोण बनाती है, तो दीवार की ऊँचाई ज्ञात कीजिए।
1.5 मीटर ऊँचाई वाला एक प्रेक्षक 22 मीटर ऊँची एक मीनार से 20.5 मीटर की दूरी पर खड़ा है। प्रेक्षक की आँख से मीनार की चोटी का उन्नयन कोण निर्धारित कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
h ऊँचाई की किसी मीनार की चोटी से दो वस्तुओं, जो मीनार के आधार वाली रेखा में स्थित हैं, के अवनमन कोण α और β (β > α) हैं। दोनों वस्तुओं के बीच की दूरी ज्ञात कीजिए।
