Advertisements
Advertisements
Question
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो की मीनार के पाद की ओर एक समान चाल से जाता है। छ: सेकेंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
Solution
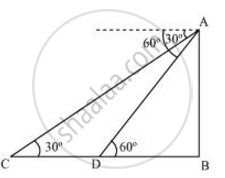
माना AB मीनार है।
कार की प्रारंभिक स्थिति C है, जो छह सेकंड के बाद D में बदल जाती है।
ΔADB में,
`("AB")/("DB") = tan 60º`
`("AB")/("DB") =sqrt3`
`"DB" = ("AB")/sqrt3`
ΔABC में,
`("AB")/("BC") = tan 30º`
`("AB")/("BD" + "DC") = 1/sqrt3`
`"AB"sqrt3 = "BD" + "DC"`
`"AB"sqrt3 = ("AB")/sqrt3 + "DC"`
`"DC" = "AB"sqrt3 - ("AB")/sqrt3 = "AB"(sqrt3 - 1/sqrt3)`
= `(2"AB")/sqrt3`
दूरी तय करने में कार द्वारा लिया गया समय DC `("i.e" "2AB"/sqrt3)` = 6 सेकंड
दूरी तय करने में कार द्वारा लिया गया समय DB `("i.e" ("AB")/sqrt3) = 6/((2"AB")/sqrt3)xx("AB")/sqrt3`
= `6/2`
= 3 सेकंड
APPEARS IN
RELATED QUESTIONS
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बिच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बिच की दूरी ज्ञात कीजिए।
यदि एक मीनार की छाया की लंबाई बढ़ रही है, तो सूर्य का उन्नयन कोण भी बढ़ रहा है।
किसी मीनार की चोटी का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दुगुनी हो जाए, तो इसकी चोटी का उन्नयन कोण भी दुगुना हो जाएगा।
सूर्य का उस समय उन्नयन कोण ज्ञात कीजिए, जब h मीटर ऊँचे एक खंभे की छाया की लंबाई `sqrt(3)` h मीटर है।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
एक ऊर्ध्वाधर मीनार एक क्षैतिज समतल पर खड़ी है तथा उस पर h ऊँचाई का एक ऊर्ध्वाधर ध्वज-दंड लगा हुआ है। समतल के किसी बिंदु से ध्वज-दंड के निचले और ऊपरी सिरों के उन्नयन कोण क्रमश : α और β हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `((h tan alpha)/(tan beta - tan alpha))` है।
