Advertisements
Advertisements
Question
ABC is an equilateral triangle . If the coordinates of A and B are (1 , 1) and (- 1 , -1) , find the coordinates of C.
Solution
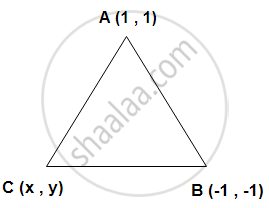
ABC is an equilateral triangle.
∴ AC = BC and AB = BC
⇒ AC2 = BC2 and AB2 = BC2
(x - 1)2 + (y - 1)2 = (x + 1)2 + (y + 1)2
⇒ x2 + 1 - 2x + y2 + 1 - 2y = x2 + 1 + 2x + y2 + 1+ 2y
⇒ - 4 x - 4y = 0
⇒ - 4 x = 4y
⇒ x = - y ...........(1)
(1 + 1)2 + (1 + 1)2 = (x + 1)2 + (y + 1)2
⇒ 8 = x2 + 1 + 2x + y2 + 1 + 2y
⇒ 8 = y2 + 1 + 2x + y2 + 1 + 2y
⇒ 2y2 - 6 = 0
⇒ y2 = 3
⇒ y = `+- sqrt 3`
From (1)
∴ x = `+- sqrt 3`
APPEARS IN
RELATED QUESTIONS
Find the distance between two points
(i) P(–6, 7) and Q(–1, –5)
(ii) R(a + b, a – b) and S(a – b, –a – b)
(iii) `A(at_1^2,2at_1)" and " B(at_2^2,2at_2)`
Find the distance between the points
(ii) A(7,-4)and B(-5,1)
Find the distance of the following point from the origin :
(8 , 15)
Find the point on y-axis whose distances from the points A (6, 7) and B (4, -3) are in the ratio 1: 2.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
Show that the quadrilateral with vertices (3, 2), (0, 5), (- 3, 2) and (0, -1) is a square.
The distance between points P(–1, 1) and Q(5, –7) is ______
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
The point which lies on the perpendicular bisector of the line segment joining the points A(–2, –5) and B(2, 5) is ______.
|
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
|
Based on the above information answer the following questions using the coordinate geometry.
- Find the distance between Lucknow (L) to Bhuj (B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P)
[OR]
Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).

