Advertisements
Advertisements
Question
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
- AD bisects BC
- AD bisects ∠A
Solution
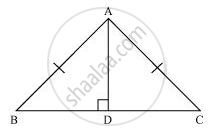
(i) In ∆ABD and ∆ACD,
AB = AC ...[Given]
∠ADB = ∠ADC ...[Each 90°]
AD = AD ...[Common]
∴ ∆ABD ≅ ∆ACD ...[By RHS Congruence Rule]
So, BD = DC ...[Corresponding parts of congruent triangles]
⇒ D is the mid-point of BC
or AD bisects BC.
(ii) Since, ∆ABD ≅ ∆ACD,
∠BAD = ∠CAD ...[Corresponding parts of congruent triangles]
⇒ Thus, AD bisects ∠A.
APPEARS IN
RELATED QUESTIONS
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
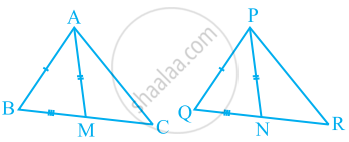
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see the given figure). Show that:
- ΔABM ≅ ΔPQN
- ΔABC ≅ ΔPQR
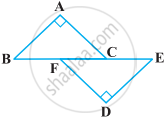
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
ABC is an isosceles triangle with AB = AC. Drawn AP ⊥ BC to show that ∠B = ∠C.
In the following figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ABC ≅ ∆DEF.
ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.
ABCD is a quadrilateral such that diagonal AC bisects the angles A and C. Prove that AB = AD and CB = CD.
ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.
